
【题目】2017年8月20日起,市交警支队全面启动路口秩序环境综合治理,重点整治机动车不礼让斑马线和行人的行为,经过一段时间的治理,从市交警队数据库中调取了20个路口近三个月的车辆违章数据,经统计得如图所示的频率分布直方图,统计数据中凡违章车次超过30次的设为“重点关注路口”.
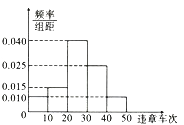
(1)现从“重点关注路口”中随机抽取两个路口安排交警去执勤,求抽出来的路口的违章车次一个在![]() ,一个在
,一个在![]() 中的概率;
中的概率;
(2)现从支队派遣5位交警,每人选择一个路口执勤,每个路口至多1人,违章车次在![]() 的路口必须有交警去,违章车次在
的路口必须有交警去,违章车次在![]() 的不需要交警过去,设去“重点关注路口”的交警人数为
的不需要交警过去,设去“重点关注路口”的交警人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为其上一点,
为其上一点,![]() 与
与![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与抛物线交于异于
与抛物线交于异于![]() 的
的![]() 两点,
两点,![]() ,
,![]() .
.
(1)求抛物线的标准方程和![]() 点的坐标;
点的坐标;
(2)判断是否存在这样的直线![]() ,使得
,使得![]() 的面积最小.若存在,求出直线
的面积最小.若存在,求出直线![]() 的方程和
的方程和![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这50件产品尺寸的样本平均数![]() .(同一组中的数据用该组区间的中点值作代表);
.(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() .
.
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则
![]() ,
,![]() ;
;
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是:
的参数方程是: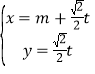 (
(![]() 是参数,
是参数,![]() 是常数).以
是常数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产品经销商销售某种鲜鱼,售价为每公斤![]() 元,成本为每公斤
元,成本为每公斤![]() 元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失
元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每公斤损失![]() 元.根据以往的销售情况,按
元.根据以往的销售情况,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到如图所示的频率分布直方图.
进行分组,得到如图所示的频率分布直方图.
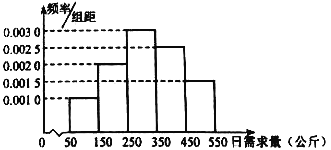
(1)求未来连续三天内,该经销商有连续两天该种鲜鱼的日销售量不低于![]() 公斤,而另一天日销售量低于
公斤,而另一天日销售量低于![]() 公斤的概率;
公斤的概率;
(2)在频率分布直方图的需求量分组中,以各组区间的中点值代表该组的各个值.
(i)求日需求量![]() 的分布列;
的分布列;
(ii)该经销商计划每日进货![]() 公斤或
公斤或![]() 公斤,以每日利润
公斤,以每日利润![]() 的数学期望值为决策依据,他应该选择每日进货
的数学期望值为决策依据,他应该选择每日进货![]() 公斤还是
公斤还是![]() 公斤?
公斤?
查看答案和解析>>
科目:高中数学 来源: 题型:
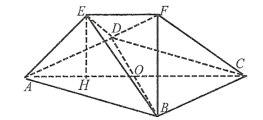
【题目】在如图所示的多面体![]() 中,底面四边形
中,底面四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 相交于
相交于![]() ,
,![]() ,
,![]() 在平面
在平面![]() 上的射影恰好是线段
上的射影恰好是线段![]() 的中点
的中点![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com