
 和
和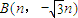 两点分别在射线OS、OT上移动,且
两点分别在射线OS、OT上移动,且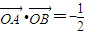 ,O为坐标原点,动点P满足
,O为坐标原点,动点P满足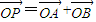 .
. ,求l的方程.
,求l的方程.
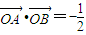 的坐标运算即可求得m•n的值;
的坐标运算即可求得m•n的值;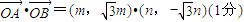
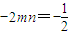
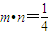 (4分)
(4分)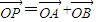
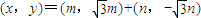 =
=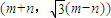 (5分)
(5分)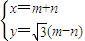 消去m,n可得
消去m,n可得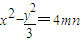 ,又因
,又因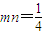 (8分)
(8分)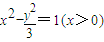
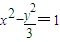 的右支(9分)
的右支(9分)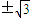 ,它与渐近线平行,不符合题意)
,它与渐近线平行,不符合题意)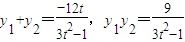
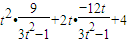
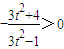

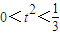 (11分)
(11分)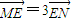 得(2-x1,-y1)=3(2-x2,y2)
得(2-x1,-y1)=3(2-x2,y2)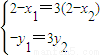
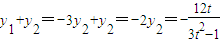 得
得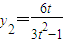
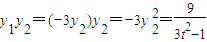 得
得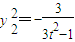
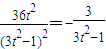
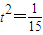 ,满足
,满足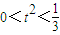 (13分)
(13分)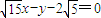 或
或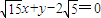 (14分)
(14分)

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
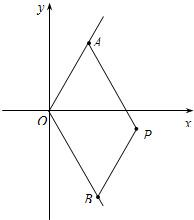 如图,A(m,
如图,A(m,| 3 |
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OP |
| OA |
| OB |
| ME |
| EN |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年绵阳市诊断三理)(12分)![]() 为坐标原点,
为坐标原点,![]() 和
和![]() 两点分别在射线
两点分别在射线![]()
![]() ≥
≥![]() 上移动,且
上移动,且![]() ,动点
,动点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() 。
。
(1)求![]() 的值;
的值;
(2)求![]() 点的轨迹
点的轨迹![]() 的方程,并说明它表示怎样的曲线?
的方程,并说明它表示怎样的曲线?
(3)设点![]() ,若直线
,若直线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两点都在以
两点都在以![]() 为圆心的圆上,求
为圆心的圆上,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
O为坐标原点, ![]() 和
和![]() 两点分别在射线
两点分别在射线![]()
![]() 上移动,且
上移动,且![]() ,动点P满足
,动点P满足![]() ,
,
记点P的轨迹为C.
(I)求![]() 的值;
的值;
(II)求P点的轨迹C的方程,并说明它表示怎样的曲线?
(III)设点G(-1,0),若直线![]() 与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求
与曲线C交于M、N两点,且M、N两点都在以G为圆心的圆上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2009年高考数学压轴试卷集锦(8)(解析版) 题型:解答题
 和
和 两点分别在射线OS、OT上移动,且
两点分别在射线OS、OT上移动,且 ,O为坐标原点,动点P满足
,O为坐标原点,动点P满足 .
. ,求l的方程.
,求l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com