
【题目】如果直线与椭圆只有一个交点,称该直线为椭圆的“切线”.已知椭圆![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的任意一点,直线
上的任意一点,直线![]() 过点
过点![]() 且是椭圆
且是椭圆![]() 的“切线”.
的“切线”.

(1)证明:过椭圆![]() 上的点
上的点![]() 的“切线”方程是
的“切线”方程是![]() ;
;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 长轴上的两个端点,点
长轴上的两个端点,点![]() 不在坐标轴上,直线
不在坐标轴上,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,过
,过![]() 的椭圆
的椭圆![]() 的“切线”
的“切线”![]() 交
交![]() 轴于点
轴于点![]() ,证明:点
,证明:点![]() 是线段
是线段![]() 的中点;
的中点;
(3)点![]() 不在
不在![]() 轴上,记椭圆
轴上,记椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,判断过
,判断过![]() 的椭圆
的椭圆![]() 的“切线”
的“切线”![]() 与直线
与直线![]() ,
,![]() 所成夹角是否相等?并说明理由.
所成夹角是否相等?并说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】试题分析:(1)联立直线和椭圆方程,由![]() ,得直线是椭圆的切线;(2)
,得直线是椭圆的切线;(2)![]() ,得
,得![]() .
. ![]() ,得
,得![]() ,过点
,过点![]() 的切线为
的切线为![]() ,得
,得![]() ,证得点
,证得点![]() 是线段
是线段![]() 的中点;(3)
的中点;(3)![]() 的方向向量
的方向向量![]() ,
,![]() ,
,![]() ,记
,记![]() 与
与![]() 的夹角
的夹角![]() ,
,![]() 与
与![]() 的夹角
的夹角![]() ,
,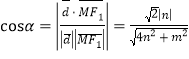 ,
, ,所以
,所以![]() ,有
,有![]() ,从而有
,从而有![]() 与直线
与直线![]() ,
,![]() 所成的夹角相等.
所成的夹角相等.
试题解析:
(1)由点![]() 在椭圆
在椭圆![]() 上,有
上,有![]() ,
,![]()
![]() 在直线
在直线![]() 上
上
当![]() 时,由
时,由![]() ,得
,得![]() ,直线方程为
,直线方程为![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,得一个交点
,得一个交点![]() ,直线
,直线![]() 是椭圆
是椭圆![]() 切线.
切线.
当![]() 时,有
时,有![]() ,直线为
,直线为![]() 代入椭圆方程得
代入椭圆方程得![]() ,有
,有![]() ,直线是椭圆
,直线是椭圆![]() 切线.
切线.
另解:不讨论将椭圆方程化为![]() ,将直线方程
,将直线方程![]() 代入消
代入消![]() ,得到
,得到![]() 的一元二次方程,然后证明
的一元二次方程,然后证明![]()
(2)![]() 点
点![]() 不在坐标轴上,
不在坐标轴上,![]() ,得
,得![]() .
. ![]() ,得
,得![]()
过点![]() 的切线为
的切线为![]() ,得
,得![]() .由
.由![]() ,得
,得![]() ,从而有
,从而有![]() ,
,![]() 点
点![]() 是线段
是线段![]() 的中点.
的中点.
(3)![]() ,
,![]() ,
,![]() 的方向向量
的方向向量![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,记
,记![]() 与
与![]() 的夹角
的夹角![]() ,
,![]() 与
与![]() 的夹角
的夹角![]() .
.
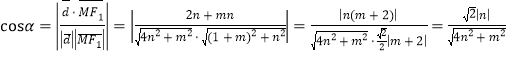 ,
,
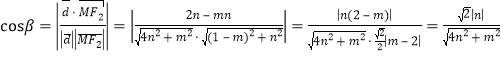 ,
,
所以![]() ,有
,有![]() ,从而有
,从而有![]() 与直线
与直线![]() ,
,![]() 所成的夹角相等.
所成的夹角相等.


科目:高中数学 来源: 题型:
【题目】【选修4-5:不等式选讲】
已知函数f(x)=|x+1|+|x-3|.
(1)若关于x的不等式f(x)<a有解,求实数a的取值范围:
(2)若关于x的不等式f(x)<a的解集为(b, ![]() ),求a+b的值.
),求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校初一年级全年级共有![]() 名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为
名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为![]() 万字.根据阅读量分组按分层抽样的方法从全年级
万字.根据阅读量分组按分层抽样的方法从全年级![]() 人中抽出
人中抽出![]() 人来作进一步调查.
人来作进一步调查.

(1)从抽出的![]() 人中选出
人中选出![]() 人来担任正副组长,求这两个组长中至少有一人的阅读量少于
人来担任正副组长,求这两个组长中至少有一人的阅读量少于![]() 万字的概率;
万字的概率;
(2)为进一步了解广泛阅读对今后学习的影响,现从抽出的![]() 人中挑选出阅读量低于
人中挑选出阅读量低于![]() 万字和高于
万字和高于![]() 万字的同学,再从中随机选出
万字的同学,再从中随机选出![]() 人来长期跟踪调查,求这
人来长期跟踪调查,求这![]() 人中来自阅读量为
人中来自阅读量为![]() 万到
万到![]() 万字的人数的概率分布列和期望值.
万字的人数的概率分布列和期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”的赞成人数如下表:
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“使用微信交流”的态度与人的年龄有关.
列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“使用微信交流”的态度与人的年龄有关.
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成的人数 | |||
不赞成的人数 | |||
合计 |
(2)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考公式:![]() ,
,![]() .
.
参考数据:
| 0.100 |
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美国对中国芯片的技术封锁激发了中国“芯”的研究热潮.某公司研发的![]() ,
,![]() 两种芯片都已经获得成功.该公司研发芯片已经耗费资金
两种芯片都已经获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产.经市场调查与预测,生产
千万元,现在准备投入资金进行生产.经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() ,其图像如图所示.
,其图像如图所示.

(1)试分别求出生产![]() ,
,![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)的函数关系式;
(千万元)的函数关系式;
(2)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() ,
,![]() 两种芯片,求可以获得的最大利润是多少.
两种芯片,求可以获得的最大利润是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的焦点分别为
)的焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,过左焦点的直线与椭圆交于
,过左焦点的直线与椭圆交于![]() ,
,![]() 两点,
两点,![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆有两个不同的交点
与椭圆有两个不同的交点![]() ,
,![]() ,且点
,且点![]() 在点
在点![]() ,
,![]() 之间,试求
之间,试求![]() 和
和![]() 面积之比的取值范围(其中
面积之比的取值范围(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求经过点P(4,1),且在两坐标轴上的截距相等的直线方程.
(2)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若|AB|=2![]() ,求圆C的面积.
,求圆C的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com