【答案】
分析:直线y=kx+1恒过定点P(0,1),且是椭圆的短轴上顶点,因而此直线被椭圆截得的弦长,即为点P与椭圆上任意一点Q的距离,设椭圆上任意一点Q(2cosθ,sinθ),利用三角函数即可得到结论.
解答:解:直线y=kx+1恒过定点P(0,1),且是椭圆的短轴上顶点,因而此直线被椭圆截得的弦长,即为点P与椭圆上任意一点Q的距离,设椭圆上任意一点Q(2cosθ,sinθ)
∴|PQ|
2=(2cosθ)
2+(sinθ-1)
2=-3sin
2θ-2sinθ+5
∴当sinθ=-

时,
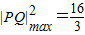
∴
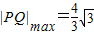
,
故选C
点评:本题考查直线与椭圆的位置关系,考查三角函数知识,解题的关键是将问题转化为点P与椭圆上任意一点Q的距离的最大值.

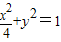 截得的最大弦长是( )
截得的最大弦长是( )
 时,
时,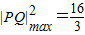
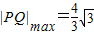 ,
,
