
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别是240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动。
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作,求事件M“抽取的2名同学来自同一年级”发生的概率。
【答案】(1) 应分别从甲、乙、丙三个年级分别抽取3人,2人,2人 (2) ![]()
【解析】
(1)由分层抽样的性质可得甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,可得抽取7名同学,应分别从甲、乙、丙三个年级分别抽取3人,2人,2人;
(2) 从抽出的7名同学中随机抽取2名的所有可能结果为21种,其中2名同学来自同一年级的所有可能结果为5种,可得答案.
解:
(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3:2:2
因为采取分层抽样的方法抽取7名同学,所以应分别从甲、乙、丙三个年级分别抽取3人,2人,2人
(2)从抽出的7名同学中随机抽取2名的所有可能结果为:
AB AC AD AE AF AG BC
BD BE BF BG CD CE CF 共21种
CG DE DF DG EF EG FG
不妨设抽出的7名同学中,来自甲年级的是A,B,C,
来自乙年级的是D,E,来自丙年级的是F,G,
则2名同学来自同一年级的所有可能结果为:
AB,AC,BC,DE,FG共5种
![]()


科目:高中数学 来源: 题型:
【题目】为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租。该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
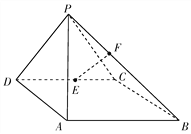
(Ⅰ)求证: ![]() ;
;
(Ⅱ)试确定点![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:an+1-an=d(n∈N*),前n项和记为Sn,a1=4,S3=21.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足b1=![]() ,bn+1-bn=2an,求数列{bn}的通项公式.
,bn+1-bn=2an,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C过点
中,椭圆C过点![]() ,焦点
,焦点![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数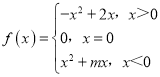 是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有
是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立,则实数a的取值范围是______.
成立,则实数a的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com