Question

已知圆台的上、下底面半径分别为r、2r，侧面积等于上、下底面积之和，则圆台的高为    ．

Answer 1

【答案】分析：求出圆台的上底面面积，下底面面积，写出侧面积表达式，利用侧面面积等于两底面面积之和，求出圆台的母线长，最后根据解直角三角形求出它的高即可．
解答：解：设圆台的母线长为l，则
圆台的上底面面积为S_上=π•r²=r²π
圆台的下底面面积为S_下=π•（2r）²=4r²π
所以圆台的两底面面积之和为S=S_上+S_下=5r²π
又圆台的侧面积S_侧=π（r+2r）l=3πrl
于是5r²π=3πrl即l=，
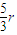
圆台的高为h==，
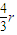
故答案为：．
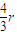
点评：本题考查旋转体（圆柱、圆锥、圆台），棱柱、棱锥、棱台的高，考查计算能力，是基础题．