练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-6-4,已知⊙O为△ABC的外接圆,AD为⊙O切线,交BC延长线于D点,求证:.

    图2-6-4

    解析:等式左侧不易降幂,设法对右侧升幂,==,故=,只需证即可.

    证法一:∵AC是弦,AD为切线,

    ∴∠CAD=∠ABC.∴△ABD∽△CAD.

    ∴.

    又由切割线定理,得DA2=DC·BD,

    ∴==.

    ∴.

    证法二:∵△ABD∽△CAD,

    ∴=.

    又△CAD与△ABD同高,∴=.

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

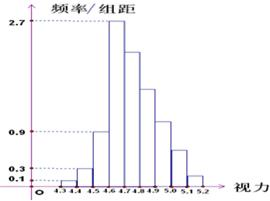    精英家教网为了研究某高校大学新生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图如图所示，已知后6组的频数从左到右依次是等差数列an的前六项．
    （1）试确定视力介于4.9至5.0的抽查学生的人数．
    （2）若规定视力低于5.0的学生属于近视学生，试估计该校新生的近视率μ的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图所示，已知点A（4，0），B（4，4），C（2，6），求AC和OB的交点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （选修4-1：几何证明选讲）
    如图所示，已知PA与⊙O相切，A为切点，PBC为割线，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且∠EDF=∠ECD．
    （1）求证：EF•EP=DE•EA；
    （2）若EB=DE=6，EF=4，求PA的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

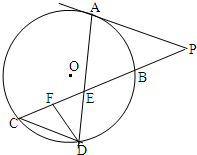    如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．
    （1）求证：∠P=∠EDF；
    （2）求证：CE•EB=EF•EP；
    （3）若CE：BE=3：2，DE=6，EF=4，求PA的长．

    查看答案和解析>>

    同步练习册答案