
【题目】椭圆中心为坐标原点O,对称轴为坐标轴,且过M(2, ![]() ) ,N(
) ,N(![]() ,1)两点,
,1)两点,
(I)求椭圆的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
【答案】(1)![]() (2)
(2)![]() ,
, ![]()
【解析】试题分析:(Ⅰ)由椭圆的离心率及过点过M(2, ![]() ) ,N(
) ,N(![]() ,1)列出方程组求出
,1)列出方程组求出![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程.
的方程.
(2)假设存在这样的圆,设该圆的切线为![]() 与椭圆联立,得
与椭圆联立,得![]() 由此利用根的判别式、韦达定理、圆的性质,结合已知条件能求出
由此利用根的判别式、韦达定理、圆的性质,结合已知条件能求出![]() 的取值范围.
的取值范围.
试题解析:(1)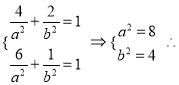
![]()
(2)假设存在这样的圆,设该圆的切线为y=kx+m,与![]() 联立消y得(1+2k2)x2+4kmx+2m2﹣8=0
联立消y得(1+2k2)x2+4kmx+2m2﹣8=0
当△=16k2m2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0
![]()
因为![]() ,所以
,所以![]()
所以3m2﹣8k2﹣8=0,由△=16k2m2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0 得
△=16k2m2﹣4(1+2k2)(2m2﹣8)=8(8k2﹣m2+4)>0
代入化简得![]()
又y=kx+m与圆心在原点的圆相切,所以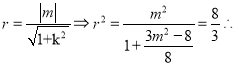 所求圆
所求圆 ![]() ,直线AB斜率不存在时也满足.
,直线AB斜率不存在时也满足.
当![]() 时,
时, 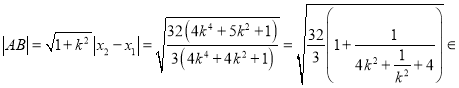
![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( ) 
A.(1,2)∪( ![]() ,3)∪(﹣∞,﹣1)
,3)∪(﹣∞,﹣1)
B.(﹣∞,﹣1)∪( ![]() ,3)
,3)
C.(﹣∞,﹣1)∪(3,+∞)
D.(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点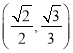 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点作斜率为
的右顶点作斜率为![]() (
(![]() )的直线交椭圆
)的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax2+bx+1(e为自然对数的底数).
(1)若 ![]() ,求函数F(x)=f(x)ex的单调区间;
,求函数F(x)=f(x)ex的单调区间;
(2)若b=e﹣1﹣2a,方程f(x)=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C的极坐标方程为ρ=6cosθ+2sinθ,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设点Q(1,2),直线l与曲线C交于A,B两点,求|QA||QB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|a﹣3x|﹣|2+x|.
(1)若a=2,解不等式f(x)≤3;
(2)若存在实数a,使得不等式f(x)≥1﹣a+2|2+x|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式a﹣ax>ex(2x﹣1)(a>﹣1)有且仅有两个整数解,则实数a的取值范围为( )
A.(﹣ ![]() ,
, ![]() ]
]
B.(﹣1, ![]() ]
]
C.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
D.(﹣ ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点A(0,4),且在两坐标轴上的截距之和为1.
(Ⅰ)求直线l的方程;
(Ⅱ)若直线l1与直线l平行,且l1与l间的距离为2,求直线l1的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com