
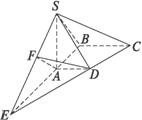
(1)求面SCD与面SBA所成的二面角的大小;
(2)求SC与平面ABCD所成的角.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.

(1)根据三视图,画出该几何体的直观图;
(2)在直观图中,①证明PD∥面AGC;②证明面PBD⊥面AGC.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省信阳市毕业班第一次调研考试文科数学试卷 题型:解答题
(本小题满分12分)请你设计一个包装盒,如下图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(cm).

(I)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.[
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com