
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
四边形,DC 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,
,
且 .
.
(1)证明:平面ACD 平面
平面 ;
;
(2)记 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求 的表达式;
的表达式;
 (3)当
(3)当 取得最大值时,求二面角D-AB-C的大小.
取得最大值时,求二面角D-AB-C的大小.
解:(1)证明:∵四边形DCBE为平行四边形 ∴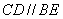 ,
,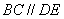 ---------1分
---------1分
∵ DC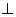 平面ABC ,
平面ABC ,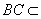 平面ABC ∴
平面ABC ∴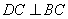 . ----------2分
. ----------2分
∵AB是圆O的直径 ∴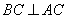 且
且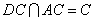
∴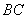
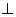 平面ADC. ∵DE//BC
∴
平面ADC. ∵DE//BC
∴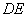
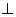 平面ADC -------------3分
平面ADC -------------3分
又∵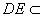 平面ADE ∴平面ACD
平面ADE ∴平面ACD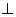 平面
平面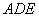 ----------------4分
----------------4分
(2)∵ DC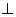 平面ABC ∴
平面ABC ∴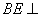 平面ABC
平面ABC
∴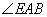 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即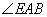 =
= -------------------5分
-------------------5分
在Rt△ABE中,由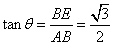 ,
,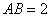 得
得 ------------6分
------------6分
在Rt△ABC中 ∵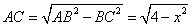 (
(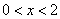 )
)
∴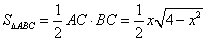 -----------------7分
-----------------7分
∴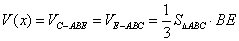
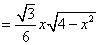 (
(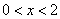 )----8分
)----8分
(3)由(2)知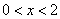
要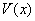 取得最大值,当且仅当
取得最大值,当且仅当 取得最大值,
取得最大值,
∵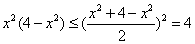 ---------------------------------------9分
---------------------------------------9分
当且仅当 ,即
,即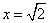 时,“=”成立,
时,“=”成立,
∴当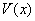 取得最大值时
取得最大值时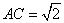 ,这时△ACB为等腰直角三角形----------10分
,这时△ACB为等腰直角三角形----------10分
 解法1:连结CO,DO
解法1:连结CO,DO
∵AC=BC,DC=DC
∴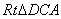 ≌
≌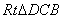 ∴AD=DB
∴AD=DB
又∵O为AB的中点 ∴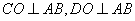
∴ 为二面角D-AB-C的平面角------------11分
为二面角D-AB-C的平面角------------11分
在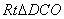 中 ∵
中 ∵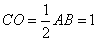 ,
,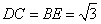
∴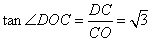 ,
∴
,
∴ =
=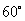
即当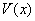 取得最大值时,二面角D-AB-C为60°.---------12分
取得最大值时,二面角D-AB-C为60°.---------12分
解法2:以点O为坐标原定,OB为x轴建立空间直角坐标系如图示:
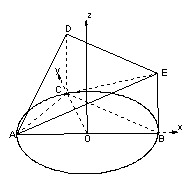 则B(1,0,0),C(0,1,0),D(0,1,
则B(1,0,0),C(0,1,0),D(0,1,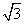 ),
∴
),
∴ ,
,
平面ABC的法向量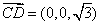 ,-------11分
,-------11分
设平面ABD的法向量为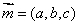
由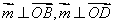 得
得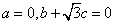
令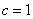 ,则
,则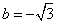 ∴
∴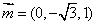 ----12分
----12分
设二面角D-AB-C的大小为 ,则
,则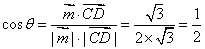
∴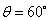 ,即二面角D-AB-C的大小为60°.---------12分
,即二面角D-AB-C的大小为60°.---------12分


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
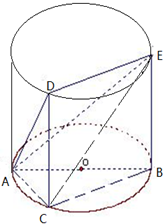 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
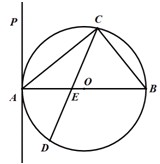 (2013•沈阳二模)选修4-1:几何证明选讲
(2013•沈阳二模)选修4-1:几何证明选讲查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com