Question

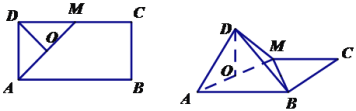
【题目】如图，在矩形ABCD中，AB=2BC=2，点M为DC的中点，将△ADM沿AM折起，使得平面△ADM⊥平面ABCM．

（1）求证：AD⊥BM；

（2）求点C到平面BDM的距离．

Answer 1

【答案】（1）见解析（2）

【解析】

（1）取AM中点O，连结DO，可得DO⊥BM，AM⊥BM，MB⊥平面ADM，即可得BM⊥AD；

（2），记点C到平面BDM的距离为h，VC﹣BDM═，又VD-BCM=VC-BDM，即可得点C到平面BDM的距离．

（1）取AM中点O，连结DO，

因为平面ADM⊥平面ABCM，AD=DM，

所以OD⊥平面ABCM，DO⊥BM，

易知AM⊥BM，

所以MB⊥平面ADM，

所以BM⊥AD；

（2）∵在矩形ADCB中，AB=2BC=2，点M为DC的中点，

∴DM=CM=，BM=AM==，DO=，

由（1）知MB⊥平面ADM，DM平面ADM，

∴BM⊥DM，S△BDM=．，

又∵DO⊥平面ABCM，

∴×=．，

记点C到平面BDM的距离为h，

∴VC-BDM═，

又∵VD-BCM=VC-BDM

∴，解得h=，

∴点C到平面BDM的距离为．