
(本题满分14分)设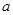 为非负实数,函数
为非负实数,函数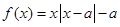 .
.
(Ⅰ)当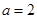 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数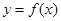 的零点个数,并求出零点.
的零点个数,并求出零点.
(Ⅰ) 的单调递增区间是
的单调递增区间是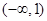 和
和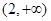 ,单调递减区间是
,单调递减区间是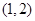
(Ⅱ)当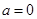 时,函数的零点为
时,函数的零点为 ;
;
当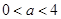 时,函数有一个零点,且零点为
时,函数有一个零点,且零点为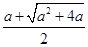 ;
;
当 时,有两个零点
时,有两个零点 和
和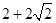 ;
;
当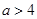 时,函数有三个零点
时,函数有三个零点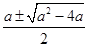 和
和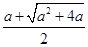 .
.
解析试题分析:(Ⅰ)当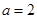 时,
时,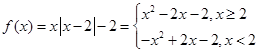 , ……2分
, ……2分
①当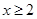 时,
时, ,∴
,∴ 在
在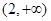 上单调递增;
上单调递增;
② 当 时,
时,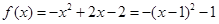 ,
,
∴ 在
在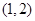 上单调递减,在
上单调递减,在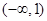 上单调递增;
上单调递增;
综上所述, 的单调递增区间是
的单调递增区间是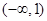 和
和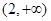 ,单调递减区间是
,单调递减区间是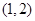 . ……6分
. ……6分
(Ⅱ)(1)当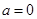 时,
时,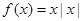 ,函数
,函数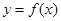 的零点为
的零点为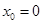 ;
;
(2)当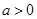 时,
时,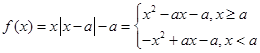 ,
,
故当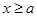 时,
时,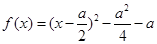 ,二次函数对称轴
,二次函数对称轴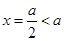 ,
,
∴ 在
在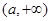 上单调递增,
上单调递增,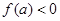 ;
;
当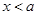 时,
时,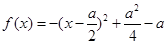 ,二次函数对称轴
,二次函数对称轴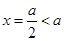 ,
,
∴ 在
在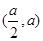 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;
∴ 的极大值为
的极大值为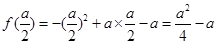 ,
, 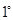 当
当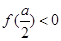 ,即
,即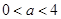 时,函数
时,函数 与
与 轴只有唯一交点,即唯一零点,
轴只有唯一交点,即唯一零点,
由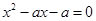 解之得
解之得
函数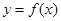 的零点为
的零点为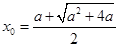 或
或 (舍去);
(舍去); 当
当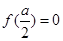 ,即
,即 时,函数
时,函数 与
与 轴有两个交点,即两个零点,分别为
轴有两个交点,即两个零点,分别为 和
和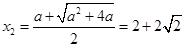 ;
;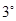 当
当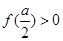 ,即
,即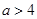 时,函数
时,函数 与
与 轴有三个交点,即有三个零点,
轴有三个交点,即有三个零点,
由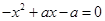 解得,
解得, ,
,
∴函数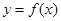 的零点为
的零点为 和
和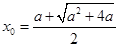 .
.
综上可得,当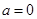 时,函数的零点为
时,函数的零点为 ;
;
当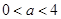 时,函数有一个零点,且零点为
时,函数有一个零点,且零点为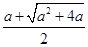 ;
;
当 时,有两个零点
时,有两个零点 和
和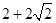 ;
;
当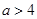 时,函数有三个零点
时,函数有三个零点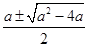 和
和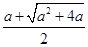 . ……14分
. ……14分
考点:本小题主要考查函数单调性的判断和单调区间的求解,含参数的二次函数单调性的判断以及函数零点个数的判断,考查学生分类讨论思想的应用.
点评:判断函数的单调性可以用单调性的定义并结合常见函数的单调性,二此函数判断单调性要结合二次函数的图象,分类讨论时要做到不重不漏.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
(本小题满分8分) 某车间生产某机器的两种配件A和B,生产配件A成本费y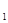 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y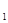 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
某商场根据调查,估计家电商品从年初(1月)开始的 个月内累计的需求量
个月内累计的需求量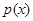 (百件)为
(百件)为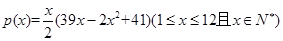
(1)求第 个月的需求量
个月的需求量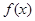 的表达式.
的表达式.
(2)若第 个月的销售量满足
个月的销售量满足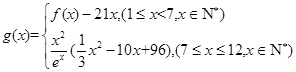 (单位:百件),每件利润
(单位:百件),每件利润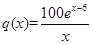 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少? 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)某单位用2 160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2 000平方米的楼房,经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)某市“环保提案”对某处的环境状况进行了实地调研,据测定,该处的污染指数与附近污染源的强度成正比,与到污染源的距离成反比,比例常数为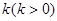 .现已知相距
.现已知相距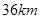 的
的 ,
, 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数 ,
, ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数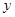 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设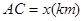 .
.
(1) 试将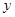 表示为
表示为 的函数;
的函数;
(2) 若 时,
时,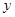 在
在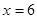 处取得最小值,试求
处取得最小值,试求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分16分)某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
(1)求函数解析式;
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为360元,那么销售价上涨了几元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设某物体一天中的温度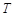 是时间
是时间 的函数:
的函数: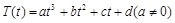 ,其中温度的单位是
,其中温度的单位是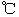 ,时间单位是小时,
,时间单位是小时,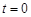 表示12:00,
表示12:00, 取正值表示12:00以后.若测得该物体在8:00的温度是
取正值表示12:00以后.若测得该物体在8:00的温度是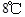 ,12:00的温度为
,12:00的温度为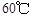 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.
(1)写出该物体的温度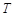 关于时间
关于时间 的函数关系式;
的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;
(3)如果规定一个函数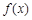 在区间
在区间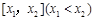 上的平均值为
上的平均值为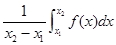 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com