
【题目】已知平面向量![]() =(1,x),
=(1,x),![]() =(2x+3,-x),x∈R.
=(2x+3,-x),x∈R.
(1)若![]() ⊥
⊥![]() ,求x的值;
,求x的值;
(2)若![]() ∥
∥![]() ,求|
,求|![]() -
-![]() |的值.
|的值.
【答案】(1)![]() 或
或![]() .(2)
.(2)![]() 或
或![]()
【解析】
(1)由![]() ⊥
⊥![]() 得其数量积等于0,从而列出关于x的方程,解方程可得x的值;
得其数量积等于0,从而列出关于x的方程,解方程可得x的值;
(2)由![]() ∥
∥![]() ,得1×(-x)-x(2x+3)=0,解出x的值,可求出
,得1×(-x)-x(2x+3)=0,解出x的值,可求出![]() 的坐标,从而可求出其模.
的坐标,从而可求出其模.
(1)若![]() ⊥
⊥![]() ,则
,则![]() ·
·![]() =(1,x)·(2x+3,-x)=1×(2x+3)+x(-x)=0
=(1,x)·(2x+3,-x)=1×(2x+3)+x(-x)=0
整理得x2-2x-3=0,解得x=-1或x=3.
(2)若![]() ∥
∥![]() ,则有1×(-x)-x(2x+3)=0,
,则有1×(-x)-x(2x+3)=0,
即x(2x+4)=0,解得x=0或x=-2.
当x=0时,![]() =(1,0),
=(1,0),![]() =(3,0),
=(3,0),![]() -
-![]() =(-2,0),
=(-2,0),
∴|![]() -
-![]() |=
|=![]() =2;
=2;
当x=-2时,![]() =(1,-2),
=(1,-2),![]() =(-1,2),
=(-1,2),![]() -
-![]() =(2,-4),
=(2,-4),
∴|![]() -
-![]() |=
|=![]() =2
=2![]()
综上,可知|![]() -
-![]() |=2或2
|=2或2![]() .
.


科目:高中数学 来源: 题型:
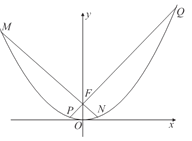
【题目】已知F为抛物线E:![]() (p>0)的焦点,C(
(p>0)的焦点,C(![]() ,1)为E上一点,且|CF|=2.过F任作两条互相垂直的直线
,1)为E上一点,且|CF|=2.过F任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线E于P,Q和M,N两点,A,B分别为线段PQ和MN的中点.
,分别交抛物线E于P,Q和M,N两点,A,B分别为线段PQ和MN的中点.
(1)求抛物线E的方程及点C的坐标;
(2)试问![]() 是否为定值?若是,求出此定值;若不是,请说明理由;
是否为定值?若是,求出此定值;若不是,请说明理由;
(3)证明直线AB经过一个定点,求此定点的坐标,并求△AOB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯将于2019年8月31日至9月15日在中国北京、广州等八座城市举行.届时,甲、乙、丙、丁四名篮球世界杯志愿者将随机分到![]() 、
、![]() 、
、![]() 三个不同的岗位服务,每个岗位至少有一名志愿者.
三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人不在同一个岗位服务的概率;
(2)设随机变量![]() 为这四名志愿者中参加
为这四名志愿者中参加![]() 岗位服务的人数,求
岗位服务的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
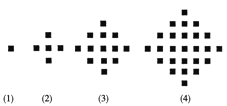
(1) 求出![]() ,
,![]() ,
,![]() 并猜测
并猜测![]() 的表达式;
的表达式;
(2) 求证:![]() +
+![]() +
+![]() +…+
+…+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,用总长为定值l的篱笆围成长方形的场地,以墙为一边,并用平行于一边的篱笆隔开.

(1)设场地面积为y,垂直于墙的边长为x,试用解析式将y表示成x的函数,并确定这个函数的定义域;
(2)怎样围才能使得场地的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进。辽宁地区也将于2020年开启新高考模式,今年秋季入学 的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为 自己将来高考“语数外+3 ”新高考方案中的“3”。某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程 组合选择一种学习。模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | ... | 40人 | ... | ... |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | ... | ... | ... | ... | ... | ... | 200人 |
为了解学生成绩与学生模拟选课情之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析.
(1)样本中选择组合12号“化生历”的有多少人?样本中选择学习物理的有多少人?
(2)从样本选择学习地理且学习物理的学生中随机抽取3人,求这3人中至少有1人还要学习生物的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与正切函数
与正切函数![]() 相邻两支曲线的交点的横坐标分别为
相邻两支曲线的交点的横坐标分别为![]() ,
, ![]() ,且有
,且有![]() ,假设函数
,假设函数![]() 的两个不同的零点分别为
的两个不同的零点分别为![]() ,
, ![]() ,若在区间
,若在区间![]() 内存在两个不同的实数
内存在两个不同的实数![]() ,
, ![]() ,与
,与![]() ,
, ![]() 调整顺序后,构成等差数列,则
调整顺序后,构成等差数列,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() 或不存在 D.
或不存在 D. ![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育主管部门到一所中学检查高三年级学生的体质健康情况,从中抽取了![]() 名学生的体质测试成绩,得到的频率分布直方图如图1所示,样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.
名学生的体质测试成绩,得到的频率分布直方图如图1所示,样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.

(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)估计该校高三学生体质测试成绩的平均数![]() 和中位数
和中位数![]() ;
;
(Ⅲ)若从成绩在![]() 的学生中随机抽取两人重新进行测试,求至少有一名男生的概率.
的学生中随机抽取两人重新进行测试,求至少有一名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com