
在三棱锥![]() 中,
中,![]() ,
,![]() .
.
求三棱锥![]() 的体积;
的体积;
证明:![]() ;
;
求异面直线SB和AC所成角的余弦值。

(1)![]()
(2)见解析
(3) ![]()
∵![]()
∴![]() 且
且![]() ,
,
∴![]() 平面
平面![]() ------------ ----------------2分
------------ ----------------2分
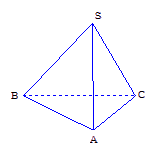 在
在![]() 中,
中, ![]() ,
,
![]() 中,
中,![]()
∵![]() ,
,
∴![]() .--------------4分
.--------------4分
(2)证法1:由(1)知SA=2, 在![]() 中,
中,![]() ---6分
---6分
∵![]() ,∴
,∴![]() -------------------8分
-------------------8分
证法2:由(1)知![]() 平面
平面![]() ,∵
,∵![]() 面
面![]() ,
,
∴![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() 面
面![]()
又∵![]() 面
面![]() ,∴
,∴![]()
(3) 解法1:分别取AB、SA、 BC的中点D、E、F,
连结ED、DF、EF、AF,则![]() ,
,
∴![]() (或其邻补角)就是异面直线SB和AC所成的角----------10分
(或其邻补角)就是异面直线SB和AC所成的角----------10分
 ∵
∵![]()
在![]() 中,
中,![]()
∴![]() ,
,
在![]() 中,
中,![]()
在△DEF中,由余弦定理得
![]()
∴异面直线SB和AC所成的角的余弦值为![]() -------------------------14分
-------------------------14分
解法2:以点A为坐标原点,AC所在的直线为y轴建立空间直角坐标系如图
则可得点A(0,0,0),C(0,1,0),B![]()
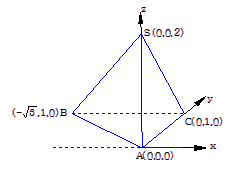 ∴
∴![]()
设异面直线SB和AC所成的角为![]()
则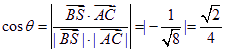
∴异面直线SB和AC所成的角的余弦值为![]() 。
。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年广东省广州市高三年级调研测试文科数学试卷(解析版) 题型:解答题
如图,在三棱锥 中,
中,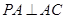 ,
,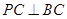 ,
,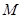 为
为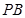 的中点,
的中点,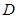 为
为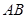 的中点,且
的中点,且 为正三角形.
为正三角形.

(1)求证: 平面
平面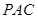 ;
;
(2)若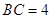 ,
,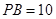 ,求点
,求点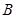 到平面
到平面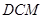 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山西省高三第一次模拟试题理科数学试卷(解析版) 题型:解答题
如图,在三棱锥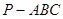 中,
中,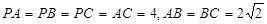

(1)求证:平面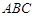 ⊥平面
⊥平面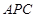
(2)求直线PA与平面PBC所成角的正弦值;
(3)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为 ,求BM的最小值.
,求BM的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西省高三第二次模拟考试文科数学试卷 题型:解答题
如图,在三棱锥 中,
中, 底面
底面 ,
, ,
, 是
是 的中点,且
的中点,且 ,
,
 .
.
(1)求证:平面 平面
平面 ;
;
(2)当角 变化时,求直线
变化时,求直线 与平面
与平面 所成的角的取值范围
所成的角的取值范围

查看答案和解析>>
科目:高中数学 来源:2010年郑州盛同学校高一下学期期末考试数学卷 题型:解答题
(本小题满分14分)如下图(5),在三棱锥 中,
中,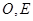 分别是
分别是 的中点,
的中点, ,
,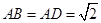 。
。
(1) 求证: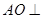 平面
平面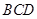 ;
;
(2) 求异面直线 与
与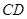 所成角的余弦值;
所成角的余弦值;
(3) 求点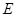 到平面
到平面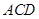 的距离。
的距离。
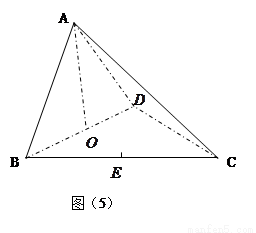
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com