

(1)写出双曲线C的离心率e与λ的关系式;
(2)当λ=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若|AB|=12,求此时的双曲线方程.
(1)解法1:设M′为PM与双曲线右准线的交点,F(c,0),则|PM|=|OF|=c,|OM|=|PF|=λc.

∵e=![]() ,|PM′|=|PM|-|MM′|=c-2
,|PM′|=|PM|-|MM′|=c-2![]() ,
,
∴e= ,即e2-λe-2=0.
,即e2-λe-2=0.
解法2:设M′为PM与双曲线右准线的交点,N为左准线与x轴的交点,F(c,0),P(x0,y0).
由于P(x0,y0)在双曲线右支上,则
x0=|PM|-|ON|=c-![]() ,①
,①
y02=![]() (x02-a2),②
(x02-a2),②
由|PF|=λc,得λ2c2=(x0-c)2+y02.③
将①②代入③得
λ2c2=(-![]() )2+
)2+![]() [(c-
[(c-![]() )2-a2].
)2-a2].
再将c=ea,b=a![]() 代入上式,得
代入上式,得
λ2e2=![]() +(e2-1)[(e-
+(e2-1)[(e-![]() )2-1],
)2-1],
化简,得λ2e2=(e2-2)2④
由题意,点P位于双曲线右支上,从而|PM|>|MM′|.于是c>2![]()
![]() ,即e2>2.
,即e2>2.
又λ>0,所以由④式得e2-λe-2=0.
(2)解:当λ=1时,由e2-e-2=0,
解得e=2.从而c=2a,b=![]() =
=![]() a.
a.
由此得双曲线的方程是![]() =1.
=1.
下面确定a的值.
解法1:设双曲线左准线与x轴的交点为N,P点的坐标为(x0,y0),则
|ON|=![]() =
=![]() ,
,
|MN|=![]()
=![]() =
=![]() a.
a.
由于P(x0,y0)在双曲线的右支上,且位于x轴上方,因而x0=|MP|-|ON|=|OF|-|ON|=c-![]() =
=![]() ,y0=|MN|=
,y0=|MN|=![]() a.
a.
所以直线OP的斜率为
k=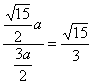 .
.
设过焦点F且平行于OP的直线与双曲线的交点为A(x1,y1)、B(x2,y2),则直线AB的斜率为k=![]() ,直线AB的方程为y=
,直线AB的方程为y=![]() (x-2a).
(x-2a).
将其代入双曲线方程整理得
4x2+20ax-29a2=0.
∵x1+x2=-5a,x1x2=-![]() a2,
a2,
∴|AB|=![]()
=![]() =12a.
=12a.
由|AB|=12,得a=1.
于是,所求双曲线的方程为x2-![]() =1.
=1.
解法2:由条件知OFPM为菱形,其对角线OP与FM互相垂直平分,其交点Q为OP的中点.
设OP的方程为y=kx(k>0),则FM的方程为y=-![]() (x-2a).
(x-2a).
由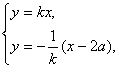
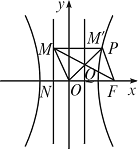
解得Q点的坐标为(![]() ).
).
所以P点的坐标为(![]() ).
).
将P点的坐标代入双曲线方程,化简得3k4+22k2-45=0.
解得k2=![]() .
.
因k>0,故k=![]() .
.
设过焦点F且平行于OP的直线与双曲线的交点为A(x1,y1)、B(x2,y2),则直线AB的斜率为k=![]() ,直线AB的方程为y=
,直线AB的方程为y=![]() (x-2a).
(x-2a).
将其代入双曲线方程,整理得4x2+20ax-29a2=0.
∵x1+x2=-5a,x1x2=-![]() a2,
a2,
∴|AB|=![]()
=![]() =12a.
=12a.
由|AB|=12,得a=1.于是,所求双曲线的方程为x2-![]() =1.
=1.


科目:高中数学 来源: 题型:044
(
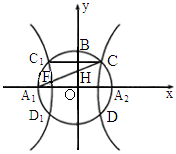
湖南长郡中学模拟)如下图,以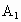 、
、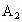 为焦点的双曲线E与半径为c的圆O相交于C、D、
为焦点的双曲线E与半径为c的圆O相交于C、D、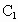 、
、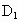 ,连接
,连接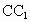 与OB交于点H,且有
与OB交于点H,且有 ,其中
,其中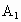 ,
,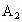 ,B是圆O与坐标轴的交点,c为双曲线的半焦距.
,B是圆O与坐标轴的交点,c为双曲线的半焦距.
(1)
当c=1时,求双曲线E的方程;(2)
试证:对任意正实数c,双曲线E的离心率为常数;(3)
连接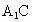 ,与双曲线E交于点F,是否存在实数λ,使
,与双曲线E交于点F,是否存在实数λ,使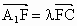 恒成立?若存在,试求出λ的值;若不存在,请说明理由.
恒成立?若存在,试求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:海南省海南中学2010-2011学年高一下学期期末考试数学试题(1班) 题型:044
阅读下列材料,解决数学问题.
圆锥曲线具有非常漂亮的光学性质,被人们广泛地应用于各种设计之中,比如椭圆镜面用来制作电影放映机的聚光灯,抛物面用来制作探照灯等,它们的截面分别是椭圆和抛物线.双曲线也具有非常好的光学性质,从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是发散的,它们好像是从另一个焦点射出的一样,如图所示.

反比例函数![]() 的图像是以直线y=x为轴,以坐标轴为渐近线的等轴双曲线,记作C.
的图像是以直线y=x为轴,以坐标轴为渐近线的等轴双曲线,记作C.
(Ⅰ)求曲线C的离心率及焦点坐标;
(Ⅱ)如下图,从曲线C的焦点F处发出的光线经双曲线反射后得到的反射光线与入射光线垂直,求入射光线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:点P在双曲线C的右准线上;
(2)求双曲线C的离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
(本题满分12分)阅读下列材料,解决数学问题.
圆锥曲线具有非常漂亮的光学性质,被人们广泛地应用于各种设计之中,比如椭圆镜面用来制作电影放映机的聚光灯,抛物面用来制作探照灯等,它们的截面分别是椭圆和抛物线.双曲线也具有非常好的光学性质,从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是发散的,它们好像是从另一个焦点射出的一样,如右上图所示.
反比例函数![]() 的图像是以直线
的图像是以直线![]() 为轴,以坐标轴为渐近线的等轴双曲线,记作C.
为轴,以坐标轴为渐近线的等轴双曲线,记作C.
(Ⅰ)求曲线C的离心率及焦点坐标;
(Ⅱ)如右下图,从曲线C的焦点F处发出的光线经双曲线反射后得到的反射光线与入射光线垂直,求入射光线的方程.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com