
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
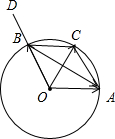
| OA |
| a |
| OB |
| b |
| a |
| π |
| 6 |
| 5π |
| 6 |
| BA |
| a |
| b |
| b |
| a |
| b |
| 5π |
| 6 |
| ||
| 3 |
| a |
| ||||
|
|
| ||
| 2 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| ||
| 3 |
| 2π |
| 3 |
| 5π |
| 6 |
| b |
| a |
| b |
| 2π |
| 3 |
| 5π |
| 6 |


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
| π |
| 8 |
| π |
| 4 |
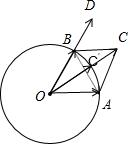
| AB |
| DC |
| BC |
| DA |
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、①③⑤ | B、④⑤ |
| C、①④⑤ | D、②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量
B.若|a|=|b|,则a、b的长度相等而方向相同或相反
C.若向量![]() 、
、![]() 满足|
满足|![]() |>|
|>|![]() |,且
|,且![]() 与
与![]() 同向,则
同向,则![]() >
>![]()
D.若两个非零向量![]() 与
与![]() 满足
满足![]() +
+![]() =0,则
=0,则![]() ∥
∥![]()
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-1 3.1空间向量及其坐标运算练习卷(解析版) 题型:填空题
下列是真命题的命题序号是 .
①分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量
②若|a|=|b|,则a,b的长度相等而方向相同或相反
③若向量 ,
, 满足|
满足| |>|
|>| |,且
|,且 与
与 同向,则
同向,则 >
>
④若两个非零向量 与
与 满足
满足 +
+ =
= ,则
,则 ∥
∥
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com