
设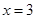 是函数
是函数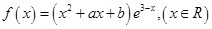 的一个极值点。
的一个极值点。
(1)求 与
与 的关系式(用
的关系式(用 表示
表示 ),并求
),并求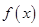 的单调区间;
的单调区间;
(2)设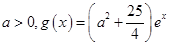 ,若存在
,若存在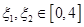 ,使得
,使得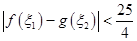 成立,求实数
成立,求实数 的取值范围。
的取值范围。
(1)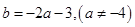 ;
;
①当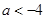 时,单增区间为:
时,单增区间为: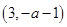 ;单减区间为:
;单减区间为: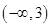 、
、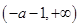 ;
;
②当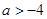 时,单增区间为:
时,单增区间为: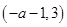 ;单减区间为:
;单减区间为: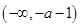 、
、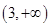 ;
;
(2) 的取值范围为
的取值范围为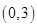 。
。
解析试题分析:(1)∵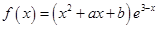 ∴
∴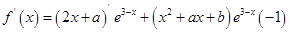
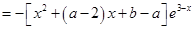 2分
2分
由题意得: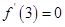 ,即
,即 ,
,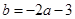 3分
3分
∴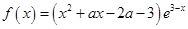 且
且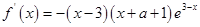
令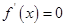 得
得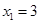 ,
,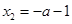
∵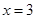 是函数
是函数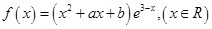 的一个极值点
的一个极值点
∴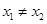 ,即
,即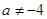
故 与
与 的关系式
的关系式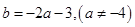 5分
5分
①当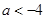 时,
时,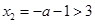 ,由
,由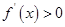 得单增区间为:
得单增区间为: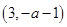 ;
;
由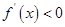 得单减区间为:
得单减区间为: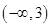 、
、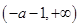 ;
;
②当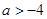 时,
时,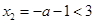 ,由
,由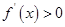 得单增区间为:
得单增区间为: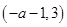 ;
;
由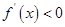 得单减区间为:
得单减区间为: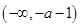 、
、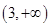 ; 8分
; 8分
(2)由(1)知:当 时,
时,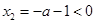 ,
,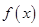 在
在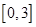 上单调递增,在
上单调递增,在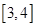 上单调递减,
上单调递减,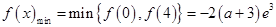 ,
,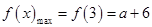
∴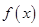 在
在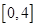 上的值域为
上的值域为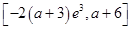 10分
10分
易知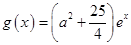 在
在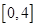 上是增函数
上是增函数
∴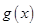 在
在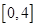 上的值域为
上的值域为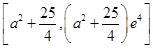 12分
12分
由于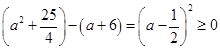 ,
,
又∵要存在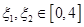 ,使得
,使得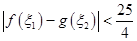 成立,
成立,
∴必须且只须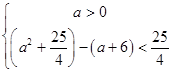 解得:
解得: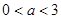
所以: 的取值范围为
的取值范围为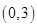 14分
14分
考点:本题主要考查应用导数研究函数的单调性及极值,确定参数的范围。
点评:典型题,本题属于导数应用中的基本问题,像涉及恒成立问题,往往通过研究函数的最值达到解题目的。证明不等式问题,往往通过构造新函数,研究其单调性及最值,而达到目的。


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
设函数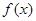 是定义在区间
是定义在区间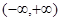 上的偶函数,且满足
上的偶函数,且满足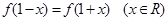
(1)求函数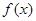 的周期;
的周期;
(2)已知当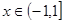 时,
时,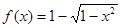 .求使方程
.求使方程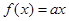 在
在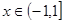 上有两个不相等实根的
上有两个不相等实根的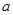 的取值集合M.
的取值集合M.
(3)记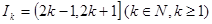 ,
,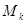 表示使方程
表示使方程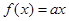 在
在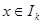 上有两个不相等实根的
上有两个不相等实根的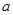 的取值集合,求集合
的取值集合,求集合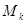 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若函数 都在区间
都在区间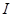 上有定义,对任意
上有定义,对任意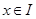 ,都有
,都有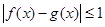 成立,则称函数
成立,则称函数 为区间
为区间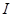 上的“伙伴函数”
上的“伙伴函数”
(1)若 为区间
为区间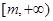 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断 是否为区间
是否为区间 上的“伙伴函数”?
上的“伙伴函数”?
(3)若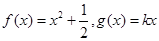 为区间
为区间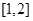 上的“伙伴函数”,求
上的“伙伴函数”,求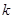 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于定义在实数集 上的两个函数
上的两个函数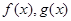 ,若存在一次函数
,若存在一次函数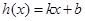 使得,对任意的
使得,对任意的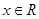 ,都有
,都有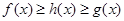 ,则把函数
,则把函数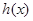 的图像叫函数
的图像叫函数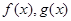 的“分界线”。现已知
的“分界线”。现已知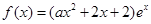 (
(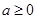 ,
,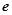 为自然对数的底数),
为自然对数的底数),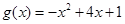
(1)求 的递增区间;
的递增区间;
(2)当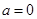 时,函数
时,函数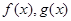 是否存在过点
是否存在过点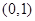 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数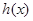 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,
OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.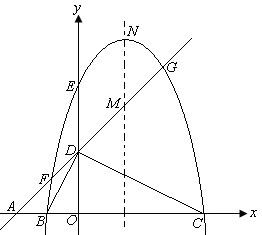
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件
的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成
为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com