
已知数列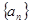 的各项均为正数,Sn为其前n项和,对于任意
的各项均为正数,Sn为其前n项和,对于任意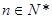 ,满足关系
,满足关系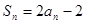 .
.
(Ⅰ)证明: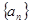 是等比数列;
是等比数列;
(Ⅱ)在正数数列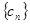 中,设
中,设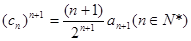 ,求数列
,求数列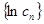 中的最大项.
中的最大项.
(1)根据数列的定义,只要证明从第二项起,每一项与前面一项的比值为定值即可。(2)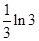
【解析】
试题分析:(Ⅰ)证明:∵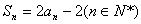 ①
①
∴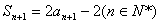 ②
②
②-①,得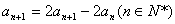
∵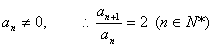 故数列
故数列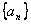 是等比数列
是等比数列
(1)由Sn=2an-2(n∈N*),知Sn-1=2an-1-2(n≥2,n∈N*),所以an=2an-2an-1.(n≥2,n∈N*),由此可知an=2n.(n∈N*).
(2)令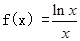 ,∵在区间(0,e)上,f'(x)>0,在区间(e,+∞)上,f'(x)<0.在区间(e,+∞)上f(x)为单调递减函数.(12分)
,∵在区间(0,e)上,f'(x)>0,在区间(e,+∞)上,f'(x)<0.在区间(e,+∞)上f(x)为单调递减函数.(12分)
∴n≥2且n∈N*时,|lncn|是递减数列.又lnc1<lnc2,∴数列|lncn|中的最大项为lnc2=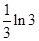
考点:等比数列的概念和数列的单调性
点评:该试题属于常规试题,主要是根据已知的关系式,变形为关于通项公式之间的递推关系,加以证明,属于基础题。


科目:高中数学 来源:2014届云南省高二9月月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知数列 的各项均为正实数,且其前
的各项均为正实数,且其前 项和
项和 满足
满足 。(1)证明:数列
。(1)证明:数列 是等差数列;
是等差数列;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市西城区高三一模试卷数学(理科) 题型:填空题
已知数列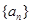 的各项均为正整数,对于
的各项均为正整数,对于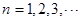 ,有
,有
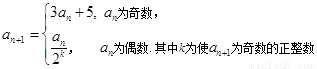 当
当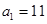 时,
时,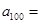 ______;
______;
若存在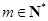 ,当
,当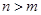 且
且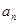 为奇数时,
为奇数时,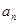 恒为常数
恒为常数 ,则
,则 的值为______.
的值为______.
查看答案和解析>>
科目:高中数学 来源:2011届北京市西城区高三一模试卷数学(理科) 题型:填空题
已知数列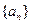 的各项均为正整数,对于
的各项均为正整数,对于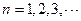 ,有
,有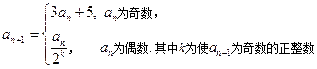 当
当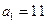 时,
时,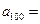 ______;
______;
若存在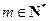 ,当
,当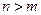 且
且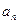 为奇数时,
为奇数时,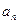 恒为常数
恒为常数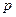 ,则
,则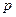 的值为______.
的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com