
已知圆C过原点且与 相切,且圆心C在直线
相切,且圆心C在直线 上.
上.
(1)求圆的方程;(2)过点 的直线l与圆C相交于A,B两点, 且
的直线l与圆C相交于A,B两点, 且 , 求直线l的方程.
, 求直线l的方程.
(1)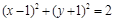 (2) x=2或4x-3y-2=0.
(2) x=2或4x-3y-2=0.
解析试题分析:(1)由题意圆心到直线 的距离等于半径, 再利用点到直线的距离公式解出圆心坐标和半径即可.(2)由题知,圆心到直线l的距离为1.分类讨论:当l的斜率不存在时,l:x=2显然成立 ;若l的斜率存在时, 利用点到直线的距离公式,解得k ;综上,直线l的方程为x=2或4x-3y-2=0.
的距离等于半径, 再利用点到直线的距离公式解出圆心坐标和半径即可.(2)由题知,圆心到直线l的距离为1.分类讨论:当l的斜率不存在时,l:x=2显然成立 ;若l的斜率存在时, 利用点到直线的距离公式,解得k ;综上,直线l的方程为x=2或4x-3y-2=0.
(1)由题意设圆心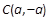 ,则C到直线
,则C到直线 的距离等于
的距离等于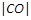 ,
,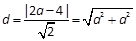 , 解得
, 解得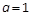 , ∴其半径
, ∴其半径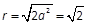
∴圆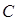 的方程为
的方程为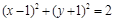 (6分)
(6分)
(2)由题知,圆心C到直线l的距离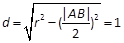 . (8分)
. (8分)
当l的斜率不存在时,l:x=2显然成立 (9分)
若l的斜率存在时,设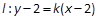 ,由
,由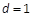 得
得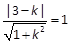 ,解得
,解得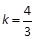 ,
,
∴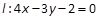 . (11分)
. (11分)
综上,直线l的方程为x=2或4x-3y-2=0. (12分)
考点:圆的方程;点到直线的距离公式.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
已知圆C的圆心在坐标原点,且与直线 相切
相切
(1)求直线 被圆C所截得的弦AB的长.
被圆C所截得的弦AB的长.
(2)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N求直线MN的方程
(3)若与直线l1垂直的直线l与圆C交于不同的两点P,Q,若∠POQ为钝角,求直线l纵截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆 过点
过点 ,
,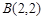 ,并且直线
,并且直线 平分圆的面积.
平分圆的面积.
(1)求圆 的方程;
的方程;
(2)若过点 ,且斜率为
,且斜率为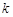 的直线
的直线 与圆
与圆 有两个不同的公共点
有两个不同的公共点 .
.
①求实数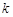 的取值范围; ②若
的取值范围; ②若 ,求
,求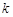 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆心为 的圆经过点
的圆经过点 .
.
(1)求圆 的标准方程;
的标准方程;
(2)若直线 过点
过点 且被圆
且被圆 截得的线段长为
截得的线段长为 ,求直线
,求直线 的方程;
的方程;
(3)是否存在斜率是1的直线 ,使得以
,使得以 被圆
被圆 所截得的弦EF为直径的圆经过
所截得的弦EF为直径的圆经过
原点?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆C经过P(4,-2),Q(-1,3)两点,且在y轴上截得的线段长为4 ,半径小于5.
,半径小于5.
(1)求直线PQ与圆C的方程;
(2)若直线l∥PQ,且l与圆C交于点A,B,且以线段AB为直径的圆经过坐标原点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆C:x2+(y-3)2=4,一动直线l过A(-1,0)与圆C相交于P、Q两点,
M是PQ中点,l与直线m:x+3y+6=0相交于N.
(1)求证:当l与m垂直时,l必过圆心C;
(2)当PQ=2 时,求直线l的方程;
时,求直线l的方程;
(3)探索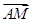 ·
· 是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
是否与直线l的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com