Question

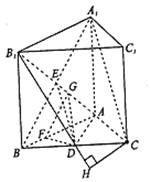
（07年西城区抽样测试理）（14分）      如图，正三棱柱ABC―A₁B₁C₁中，D是BC的中点，AA₁=AB=1.

   

    （I）求证：A₁C//平面AB₁D；

   （II）求二面角B―AB₁―D的大小；

   （III）求点c到平面AB₁D的距离.

 

Answer 1

解析：解法一（I）证明：

连接A₁B，设A₁B∩AB₁ = E，连接DE.

∵ABC―A₁B₁C₁是正三棱柱，且AA₁ = AB，

∴四边形A₁ABB₁是正方形，

∴E是A₁B的中点，

又D是BC的中点，

∴DE∥A₁C. ………………………… 3分

∵DE平面AB₁D，A₁C平面AB₁D，

∴A₁C∥平面AB₁D. ……………………4分

   （II）解：在面ABC内作DF⊥AB于点F，在面A₁ABB₁内作FG⊥AB₁于点G，连接DG.

∵平面A₁ABB₁⊥平面ABC，  ∴DF⊥平面A₁ABB₁，

∴FG是DG在平面A₁ABB₁上的射影，  ∵FG⊥AB₁， ∴DG⊥AB₁

∴∠FGD是二面角B―AB₁―D的平面角 …………………………7分

设A₁A = AB = 1，在正△ABC中，DF=

在△ABE中，，

在Rt△DFG中，，

所以，二面角B―AB₁―D的大小为 …………………………9分

   （III）解：∵平面B₁BCC₁⊥平面ABC，且AD⊥BC，

∴AD⊥平面B₁BCC₁，又AD平面AB₁D，∴平面B₁BCC₁⊥平面AB₁D.

在平面B₁BCC₁内作CH⊥B₁D交B₁D的延长线于点H，

则CH的长度就是点C到平面AB₁D的距离. ……………………………12分

由△CDH∽△B₁DB，得

即点C到平面AB₁D的距离是 ……………………………………14分

解法二：

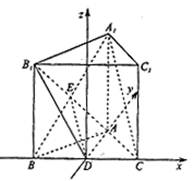
建立空间直角坐标系D―xyz，如图，

   （I）证明：

连接A₁B，设A₁B∩AB₁ = E，连接DE.

设A₁A = AB = 1，

则

 …………………………3分

，

 ……………………………………4分

   （II）解：， ，

设是平面AB₁D的法向量，则，

故；

同理，可求得平面AB₁B的法向量是 ……………………7分

设二面角B―AB₁―D的大小为θ，，

∴二面角B―AB₁―D的大小为 …………………………9分

   （III）解由（II）得平面AB₁D的法向量为，

取其单位法向量

∴点C到平面AB₁D的距离 ……………………14分