Question

【题目】（分）如图，在三棱锥中，底面为等边三角形，，，为的中点．

（Ⅰ）求证：．

（Ⅱ）判断在线段上是否存在点（与点不重合），使得为直角三角形？若存在，试找出一个点，并求的值；若不存在，说明理由．

Answer 1

【答案】（1）详见解析（2）当时，为直角三角形．

【解析】

试题分析：（1）根据正三角形的性质可得，根据勾股定理可得，由线面垂直证的判定定理可得平面，由线面垂直的性质可得结论；（2）在（1）基础上可知平面与平面的垂直性，所以只需过作交线的垂线，由线线垂直线面垂直，再由线面垂直线线垂直，证明直角三角形的存在性，在上述条件下分别求出，，从而求出的值即可.

试题解析：

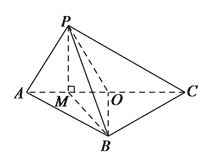
（Ⅰ）证明：如图，连结，

∵在等边中，是的中点，且，

∴，，

∵在直角中，是斜边的中点，且，

∴，

在中，由，得，

∴，

又∵，平面，平面，

∴平面，

又∵平面，

∴．

（Ⅱ）解：线段上存在点使得为直角三角形，此时，

如图，过作于点，连结，

∵平面，

∴，

又∵，平面，平面，

∴平面，

∴，

即为直角三角形，

故当点与点重合时，为直角三角形，

在直角中，由，，，

得（即），（即），

当时，为直角三角形．

【方法点晴】本题主要考查线面垂直性质与判定、线线垂直的证明，属于难题. 证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.本题的解答一直围绕线面垂直与线线垂直的互相转化进行.