
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,且
的中点,且![]() 为正三角形.
为正三角形.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,
, ![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 与平面
与平面![]() 内的两条相交直线
内的两条相交直线![]() 垂直,利用直线与平面垂直的判定定理证明即可;
垂直,利用直线与平面垂直的判定定理证明即可;
(2)解法一:通过![]() ,利用等体积法
,利用等体积法![]() ,即可求解点
,即可求解点![]() 到平面
到平面![]() 的距离;
的距离;
解法二:过点![]() 作直线
作直线![]() 的垂线,角
的垂线,角![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() 平面
平面![]() ,说明
,说明![]() 为点
为点![]() 到平面
到平面![]() 的距离,一是利用等面积求解,二是利用解直角三角形求解.
的距离,一是利用等面积求解,二是利用解直角三角形求解.
试题解析:
(![]() )
)
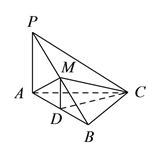
证明:在正![]() 中,
中, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,故
,故![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )解法
)解法![]() :设点
:设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() ,
, ![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 为正三角形,
为正三角形,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵ .
.
由(![]() )知
)知![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.



 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】以下是新兵训练时,某炮兵连8周中炮弹对同一目标的命中情况的柱状图: 
(1)计算该炮兵连这8周中总的命中频率p0 , 并确定第几周的命中频率最高;
(2)以(1)中的p0作为该炮兵连炮兵甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射3次,记命中的次数为X,求X的数学期望;
(3)以(1)中的p0作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99?(取lg0.4=﹣0.398)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|![]() |;
|;
(2)已知点D是AB上一点,满足![]() =λ
=λ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足![]() =λ
=λ![]() .
.
①当λ=![]() 时,求
时,求![]()
![]() ;
;
②是否存在非零实数λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率为
的中心在原点,离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆下顶点为![]() ,直线
,直线![]() (
(![]() )与椭圆相交于不同的两点
)与椭圆相交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某班一次测验成绩进行统计,如下表所示:
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
概率 | 0.02 | 0.04 | 0.17 | 0.36 | 0.25 | 0.15 |
(1)求该班成绩在[80,100]内的概率;
(2)求该班成绩在[60,100]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2(a∈R).
x2(a∈R).
(1)若x>0,恒有f(x)≤x成立,求实数a的取值范围;
(2)若a=0,求f(x)在区间[t,t+2](t>0)上的最小值;
(3)若函数g(x)=f(x)﹣x有两个极值点x1 , x2 , 求证: ![]() +
+ ![]() >2ae.
>2ae.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )
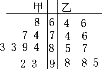
A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com