练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设(2x-1)5=a0+a1x+a2x2+…+a5x5,求:

    (1)a0+a1+a2+a3+a4;

    (2)|a0|+|a1|+|a2|+|a3|+|a4|+|a5|;

    (3)a1+a3+a5;

    (4)(a0+a2+a4)2-(a1+a3+a5)2.

    剖析:(2x-1)5=a0+a1x+a2x2+…+a5x5为关于x的恒等式,求系数和的问题可用赋值法解决.

    解:设f(x)=(2x-1)5=a0+a1x+a2x2+…+a5x5,则f(1)=a0+a1+a2+…+a5=1,

        f(-1)=a0-a1+a2-a3+a4-a5=(-3)5=-243.

        (1)∵a5=25=32,

        ∴a0+a1+a2+a3+a4=f(1)-32=-31.

        (2)|a0|+|a1|+|a2|+…+|a5|=-a0+a1-a2+a3-a4+a5=-f(-1)=243.

        (3)∵f(1)-f(-1)=2(a1+a3+a5),

        ∴a1+a3+a5==122.

        (4)(a0+a2+a4)2-(a1+a3+a5)2

        =(a0+a1+a2+a3+a4+a5)(a0-a1+a2-a3+a4-a5)=f(1)×f(-1)=243.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意的x∈[a，b]，都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“亲密函数”，区间[a，b]称为“亲密区间”．若f（x）=x2-3x+2与g（x）=2x-1在[a，b]上是“紧密函数”，则其“紧密区间”可以是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设实数集R为全集，A={x|0≤2x-1≤5}，B={x|x2+a＜0}．
    （1）当a=-4时，求A∩B及A∪B；
    （2）若B∩（?RA）=B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    设f(x)＝(2x＋1)5-5(2x＋1)4＋10(2x＋1)3-10(2x＋1)2＋5(2x＋1)-1，则f(x)等于（　）

    A．(2x＋2)5

    B．32x5

    C．(2x-1)5

    D．2x5

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年安徽省安庆市望江二中高三（上）第一次月考数学试卷（理科）（解析版） 题型：填空题

    设（1-x）（1+2x）5=a+a1x+a2x2+…+a6x6，则a2=    ．

    查看答案和解析>>

    科目：高中数学 来源：2013届福建省泉州市高二下学期期中文科数学试卷（解析版） 题型：解答题

    已知二次函数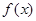的二次项系数为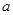，且不等式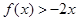的解集为,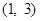

    （1）若方程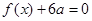有两个相等的根，求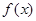的解析式；

    （2）若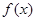的最大值为正数，求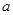的取值范围．

    【解析】第一问中利用∵f(x)+2x>0的解集为(1,3),

    设出二次函数的解析式，然后利用判别式得到a的值。

    第二问中，

    解：（1）∵f(x)+2x>0的解集为(1,3),

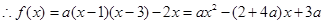       ①

    由方程

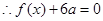
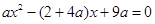                  ②

    ∵方程②有两个相等的根，

    ∴，

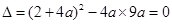    即5a2-4a-1=0,解得a=1(舍) 或 a=-1/5

    a=-1/5代入①得：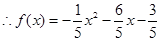

    （2）由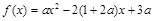

     

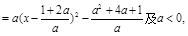
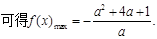
    由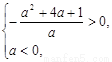 解得：

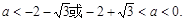
    故当f(x)的最大值为正数时，实数a的取值范围是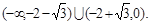

     

    查看答案和解析>>

    同步练习册答案