
【题目】已知函数 ![]() 是偶函数,g(x)=t2x+4,
是偶函数,g(x)=t2x+4,
(1)求a的值;
(2)当t=﹣2时,求f(x)<g(x)的解集;
(3)若函数f(x)的图象总在g(x)的图象上方,求实数t的取值范围.
【答案】
(1)解:由f(x)是偶函数,得f(x)=f(﹣x),即 ![]() ,
,
化简得22ax=4x,故a=1
(2)解:f(x)<g(x)即 ![]() ,亦即34x﹣42x+1<0,
,亦即34x﹣42x+1<0,
所以 ![]() ,即
,即 ![]() ,
,
所以不等式f(x)<g(x)的解集为 ![]()
(3)解:因为函数f(x)的图象总在g(x)的图象上方,
所以f(x)>g(x),即 ![]() ,得
,得 ![]() ,
,
∵ ![]() ,∴t<﹣3;
,∴t<﹣3;
故实数t的取值范围为:t<﹣3
【解析】(1)由偶函数的定义知f(x)=f(﹣x),化简即可求得a值;(2)对f(x)<g(x)进行等价变形可化为关于2x的二次不等式,解得2x的范围,进而可得x的范围;(3)函数f(x)的图象总在g(x)的图象上方,等价于f(x)>g(x)恒成立,分离出t后转化为求函数的最值解决;
【考点精析】本题主要考查了函数单调性的性质和复合函数单调性的判断方法的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能正确解答此题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一函数的是( )
A.y=1,y= ![]()
B.y= ![]() ×
× ![]() ,y=
,y= ![]()
C.y=2x+1﹣2x , y=2x
D.y=2lgx,y=lgx2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() (
(![]() ),与
),与![]() 图象的对称轴
图象的对称轴![]() 相邻的
相邻的![]() 的零点为
的零点为![]() .
.
(Ⅰ)讨论函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(Ⅱ)设![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对应边分别为
的对应边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,若向量
,若向量![]() 与向量
与向量![]() 共线,求
共线,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1 , 底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别为A1B1、A1A的中点. 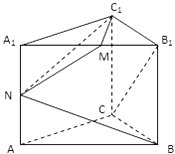
(1)求 ![]() >的值;
>的值;
(2)求证:BN⊥平面C1MN;
(3)求点B1到平面C1MN的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣3x+(a﹣1)lnx,g(x)=ax,h(x)=f(x)﹣g(x)+3x.
x2﹣3x+(a﹣1)lnx,g(x)=ax,h(x)=f(x)﹣g(x)+3x.
(1)当a=5时,求函数f(x)的导函数f′(x)的最小值;
(2)当a=3时,求函数h(x)的单调区间及极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中球的二维测度(表面积)S=4πr2 , 三维测度(体积)V= ![]() πr3;四维空间中“超球”的三维测度V=8πr3 , 则猜想其四维测度W= .
πr3;四维空间中“超球”的三维测度V=8πr3 , 则猜想其四维测度W= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,圆
的任意一点,圆![]() 在点
在点![]() 处的切线与圆
处的切线与圆![]() 在点
在点![]() 处的切线分别交于
处的切线分别交于![]() ,直线
,直线![]() 和
和![]() 交于点
交于点![]() ,设
,设![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
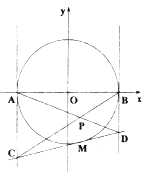
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴正半轴交点为
轴正半轴交点为![]() ,则曲线
,则曲线![]() 是否存在直角顶点为
是否存在直角顶点为![]() 的内接等腰直角三角形
的内接等腰直角三角形![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 的两条直角边所在直线的方程,若不存在,请说明理由.
的两条直角边所在直线的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com