
【题目】已知动圆![]() 恒过点
恒过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() (
(![]() 为坐标原点)分别交直线
为坐标原点)分别交直线![]() 于点
于点![]() ,
, ![]() ,证明:以
,证明:以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长为定值.
轴截得的弦长为定值.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)分析题意,由抛物线的定义,可知圆心![]() 的轨迹为以
的轨迹为以![]() 为焦点,
为焦点, ![]() 为准线的抛物线,且
为准线的抛物线,且![]() ,圆心C的轨迹方程为
,圆心C的轨迹方程为![]() ;(2)设
;(2)设![]() ,由A,P,B三点共线,求出
,由A,P,B三点共线,求出![]() ,以MN为直径的圆的方程为
,以MN为直径的圆的方程为 ,化简得
,化简得![]() ,令
,令![]() ,求出
,求出![]() 的值,求出弦长。
的值,求出弦长。
试题解析:
(1)由题意得,点![]() 与点
与点![]() 的距离始终等于点
的距离始终等于点![]() 到直线
到直线![]() 的距离.
的距离.
因此由抛物线的定义,可知圆心![]() 的轨迹为以
的轨迹为以![]() 为焦点,
为焦点, ![]() 为准线的抛物线.
为准线的抛物线.
所以![]() ,即
,即![]() .
.
所以圆心![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)由圆心![]() 的轨迹方程为
的轨迹方程为![]() ,
,
可设![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
由![]() ,
, ![]() ,
, ![]() 三点共线,可知
三点共线,可知![]() ,
,
即![]() .
.
因为![]() ,所以
,所以![]() .
.
又依题得,直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得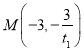 .
.
同理可知 .
.
因此以![]() 为直径的圆的方程可设为
为直径的圆的方程可设为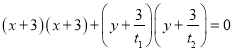 .
.
化简得 ,
,
即![]() .
.
将![]() 代入上式,可知
代入上式,可知![]() ,
,
在上式中令![]() ,可知
,可知![]() ,
, ![]() ,
,
因此以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长为
轴截得的弦长为![]() ,为定值.
,为定值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程![]() 关于时间
关于时间![]() 的函数关系式分别为
的函数关系式分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,有以下结论:
,有以下结论:
①当![]() 时,甲走在最前面;
时,甲走在最前面;
②当![]() 时,乙走在最前面;
时,乙走在最前面;
③当![]() 时,丁走在最前面,当
时,丁走在最前面,当![]() 时,丁走在最后面;
时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中四边形ABCD为矩形,E,F分别为PA,PD的中点,在此几何体中,给出下面4个结论:

![]() 直线BE与直线CF异面;
直线BE与直线CF异面;![]() 直线BE与直线AF异面;
直线BE与直线AF异面;![]() 直线
直线![]() 平面PBC;
平面PBC;![]() 平面
平面![]() 平面PAD.
平面PAD.
其中正确的结论个数为![]()
![]()
A. 4个
B. 3个
C. 2个
D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,![]() ,PA=AC=1.
,PA=AC=1.
(1)求证:AE⊥PB;
(2)求三棱锥C-ABE的体积.
(3)求二面角A-PB-C的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 分别为函数
分别为函数![]() 的导函数.若存在
的导函数.若存在![]() ,满足
,满足![]() 且
且![]() ,则称
,则称![]() 为函数
为函数![]() 与
与![]() 的一个“S点”.
的一个“S点”.
(1)证明:函数![]() 与
与![]() 不存在“S点”;
不存在“S点”;
(2)若函数![]() 与
与![]() 存在“S点”,求实数a的值;
存在“S点”,求实数a的值;
(3)已知函数![]() ,
,![]() .对任意
.对任意![]() ,判断是否存在
,判断是否存在![]() ,使函数
,使函数![]() 与
与![]() 在区间
在区间![]() 内存在“S点”,并说明理由.
内存在“S点”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,下列四个命题中正确的是( )
,下列四个命题中正确的是( )
A.若![]() ,则
,则![]() 一定是锐角三角形
一定是锐角三角形
B.若![]() ,则
,则![]() 一定是等边三角形
一定是等边三角形
C.若![]() ,则
,则![]() 一定是等腰三角形
一定是等腰三角形
D.若![]() ,则
,则![]() 一定是等腰三角形
一定是等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com