
 设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.| OM |
| ON |
| OM |
| ON |
| OM |
| ON |
| 4-4d1d2sin2θ |
| 1-λ |
| 1-λ |
| x2 |
| 1-λ |
| y2 |
| λ |
| 1 |
| 1-λ |
| 1 |
| λ |
-1±
| ||
| 2 |
| ||
| 2 |
|
| -2k2(1-λ) |
| λ-(1-λ)k2 |
| -(1-λ)(k2+λ) |
| λ-(1-λ)k2 |
| k2λ2 |
| λ-(1-λ)k2 |
| OM |
| ON |
|
|
|
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:044
(2007
江西,21)设动点P到点A(-1,0)和B(1,0)的距离分别为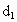 和
和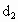 ,∠APB=2θ,且存在常数λ(0<λ<1),使得
,∠APB=2θ,且存在常数λ(0<λ<1),使得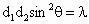 .
.
(1)
证明:动点P的轨迹C为双曲线,并求出C的方程;(2)
过点B作直线交双曲线C的右支于M、N两点,试确定λ的范围,使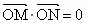 ,其中点O为坐标原点.
,其中点O为坐标原点.查看答案和解析>>
科目:高中数学 来源:吉林省长春市十一高2011-2012学年高二下学期期中考试数学理科试题 题型:013
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2![]() ,且存在常数λ(0<λ<1),使得
,且存在常数λ(0<λ<1),使得![]() .(如图所示)那么点P的轨迹是
.(如图所示)那么点P的轨迹是
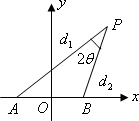
A.圆
B.椭圆
C.双曲线
D.抛物线
查看答案和解析>>
科目:高中数学 来源:湖北省武汉四中2008届高三九月考模拟试题、数学 题型:044
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,![]() ,且存在常数λ(0<λ<1),使得
,且存在常数λ(0<λ<1),使得![]() .
.
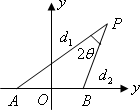
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线双曲线C的右支于M,N两点,试确定λ的范围,使![]() ,其中点O为坐标原点.
,其中点O为坐标原点.
查看答案和解析>>
科目:高中数学 来源:2007年江西省高考数学试卷(理科)(解析版) 题型:解答题
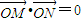 ,其中点O为坐标原点.
,其中点O为坐标原点.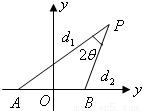
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com