
【题目】如图1,在高为2的梯形ABCD中,![]() ,
,![]() ,
,![]() ,过A、B分别作
,过A、B分别作![]() ,
,![]() ,垂足分别为E、
,垂足分别为E、![]() 已知
已知![]() ,将D、C沿AE、BF折向同侧,得空间几何体
,将D、C沿AE、BF折向同侧,得空间几何体![]() ,如图2.
,如图2.

![]() 若
若![]() ,求证:
,求证:![]() ;
;
![]() 若
若![]() ,线段AB的中点是P,求CP与平面ACD所成角的正弦值.
,线段AB的中点是P,求CP与平面ACD所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
![]() 由已知得四边形ABEF是正方形,且边长为2,取BE与AF的交点为O,推导出
由已知得四边形ABEF是正方形,且边长为2,取BE与AF的交点为O,推导出![]() ,
,![]() ,从而
,从而![]() 平面BDE,进而
平面BDE,进而![]() ,再由
,再由![]() ,得
,得![]() 平面ABEF,从而
平面ABEF,从而![]() .
.
![]() 以E为原点,EA为x轴,EF为y轴,ED为z轴,建立空间直角坐标系,利用向量法能求出CP与平面ACD所成角的正弦值.
以E为原点,EA为x轴,EF为y轴,ED为z轴,建立空间直角坐标系,利用向量法能求出CP与平面ACD所成角的正弦值.
证明:![]() 由已知得四边形ABEF是正方形,且边长为2
由已知得四边形ABEF是正方形,且边长为2
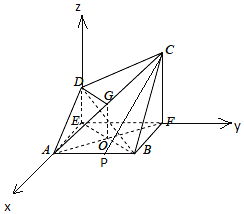
在图2中,取BE与AF的交点为O,则![]() ,
,
由已知得![]() ,
,![]() ,
,![]() 平面BDE,
平面BDE,
又![]() 平面BDE,
平面BDE,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面ABEF,
平面ABEF,
又![]() 平面ABEF,
平面ABEF,![]() .
.
解:![]() 以E为原点,EA为x轴,EF为y轴,ED为z轴,
以E为原点,EA为x轴,EF为y轴,ED为z轴,
建立空间直角坐标系,
![]() 2,
2,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
![]() 0,
0,![]() ,
,
![]() ,
,![]() 0,
0,![]() ,
,![]() 2,
2,![]() ,
,
设平面ACD的法向量![]() y,
y,![]() ,
,
则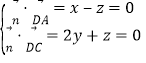 ,
,
取![]() ,得
,得![]() ,
,
设CP与平面ACD所成角为![]() .
.
则![]() .
.
![]() 与平面ACD所成角的正弦值为
与平面ACD所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
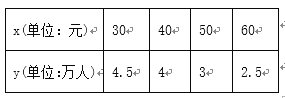
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: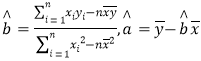
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 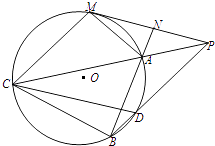
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}满足b3=3,b5=9.
(1)分别求数列{an},{bn}的通项公式;
(2)设Cn= ![]() (n∈N*),求证Cn+1<Cn
(n∈N*),求证Cn+1<Cn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:动点P,Q都在曲线C: ![]() (t为参数)上,对应参数分别为t=α与t=2α(0<α<2π),M为PQ的中点.
(t为参数)上,对应参数分别为t=α与t=2α(0<α<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=﹣sin(ωx+φ)(ω>0,φ∈(﹣ ![]() ,
, ![]() ))的一条对称轴为x=
))的一条对称轴为x= ![]() ,一个对称中心为(
,一个对称中心为( ![]() ,0),在区间[0,
,0),在区间[0, ![]() ]上单调.
]上单调.
(1)求ω,φ的值;
(2)用描点法作出y=sin(ωx+φ)在[0,π]上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
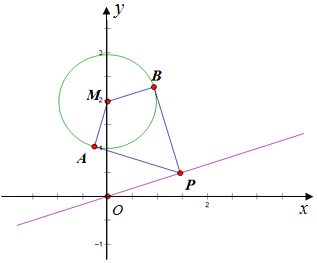
![]() 若
若![]() ,试求点P的坐标;
,试求点P的坐标;
![]() 求四边形PAMB面积的最小值及此时点P的坐标;
求四边形PAMB面积的最小值及此时点P的坐标;
![]() 求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标.
求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题,其中正确命题的个数( )
①若a>|b|,则a2>b2
②若a>b,c>d,则a﹣c>b﹣d
③若a>b,c>d,则ac>bd
④若a>b>o,则 ![]() >
> ![]() .
.
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com