
(Ⅰ)证明:12S3、S6、S12-S6成等比数列;
(Ⅱ)求和:Tn=a1+2a4+3a7+…+na3n-2.
20.(Ⅰ)证明:由a1、2a7、3a4成等差数列.
得4a7=a1+3a4,即4aq6=a+3aq3.
变形得(4q3+1)(q3-1)=0,所以q3=-![]() 或q3=1(舍去).
或q3=1(舍去).
由![]() =
=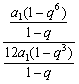 =
=![]() =
=![]() ,
,
![]() =
=![]() -1=
-1=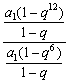 -1=1+q6-1=q6=
-1=1+q6-1=q6=![]() ,
,
得![]() =
=![]() .
.
所以12S3,S6,S12-S6成等比数列.
(Ⅱ)解 Tn=a1+2a4+3a7+…+na3n-2
=a+2aq3+3aq6+…+naq3(n-1),
即Tn=a+2·(-![]() )a+3·(-
)a+3·(-![]() )2a+…+n·(-
)2a+…+n·(-![]() )n-1a. ①
)n-1a. ①
①×(-![]() )得
)得
-![]() Tn=-
Tn=-![]() a+2·(-
a+2·(-![]() )2a+3·(-
)2a+3·(-![]() )3a+…+n·(-
)3a+…+n·(-![]() )na. ②
)na. ②
①-②有:![]() Tn=a+(-
Tn=a+(-![]() ) a+(-
) a+(-![]() )2a+(-
)2a+(-![]() )3a+…+(-
)3a+…+(-![]() )n-1a-n·(-
)n-1a-n·(-![]() )na
)na
=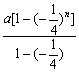 -n·(-
-n·(-![]() )na
)na
=![]() a-(
a-(![]() +n)·(-
+n)·(-![]() )na.
)na.
所以Tn=![]() a-(
a-(![]() +
+![]() n)·(-
n)·(-![]() )na.
)na.


科目:高中数学 来源: 题型:阅读理解
| n |
 |
| k=1 |
| 1 |
| lg(ak+2)lg(ak+1+2) |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求和:a1![]() -a2
-a2![]() +a3
+a3![]() ,a1
,a1![]() -a2
-a2![]() +a3
+a3![]() -a4
-a4![]() ;
;
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com