【答案】
分析:(Ⅰ)用数学归纳法证明0<a
n<1,n∈N
*.(1)当n=1时,由已知得结论成立;(2)假设当n=k时,结论成立,即0<a
k<1.则当n=k+1时,因为0<x<1时,f′(x)=1-

=
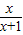
>0,所以f(x)在(0,1)上是增函数.可和f(0)<f(a
k)<f(1),即0<a
k+1<1<1-ln2<1.再由a
n+1-a
n=an-ln(1+a
n)-an=-ln(1+a
n)<0,有a
n+1<a
n.进而得到结论.
(Ⅱ)根据问题和a
n+1=f(a
n),可构造函数g(x)=
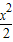
-f(x)=
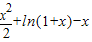
,0<x<1,即证g(x)>0成立,用导数法研究因为g′(x)=
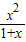
>0,知g(x)在(0,1)上增函数.得到结论.
(Ⅲ)由b
1=

,b
n+1≥

(n+1)b
n,可再由b
n>0,变形为
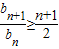
,从而由累乘法可得b
n=
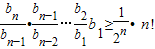
①,再由a
n+1<
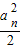
推知:
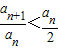
,再用累乘法可得
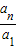
=
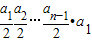
<
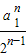
<
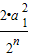
=
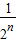
②.由①②两式可得结论.
解答:解:(Ⅰ)先用数学归纳法证明0<a
n<1,n∈N
*.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即0<a
k<1.则当n=k+1时,
∵0<x<1时,f′(x)=1-
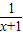
=
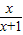
>0,
∴f(x)在(0,1)上是增函数.
又∵f(x)在[0,1]上连续,
∴f(0)<f(a
k)<f(1),即0<a
k+1<1<1-ln2<1.
故当n=k+1时,结论也成立.即0<a
n<1对于一切正整数都成立.(4分)
又由0<a
n<1,得a
n+1-a
n=an-ln(1+a
n)-an=-ln(1+a
n)<0,从而a
n+1<a
n.
综上可知0<a
n+1<a
n<1(6分)
(Ⅱ)构造函数g(x)=
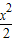
-f(x)=
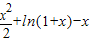
,0<x<1,
由g′(x)=
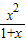
>0,知g(x)在(0,1)上增函数.
又g(x)在[0,1]上连续,
∴g(x)>g(0)=0.
∵0<a
n<1,
∴g(a
n)>0,即
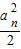
-f(an)>0,
从而a
n+1<
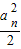
(10分)
(Ⅲ)∵b
1=

,b
n+1≥

(n+1)b
n,
∴b
n>0,
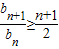
,
∴b
n=
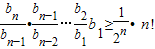
①,(12分)
由(Ⅱ)a
n+1<
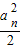
知:
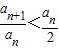
,
∴
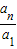
=
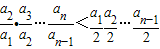
,
∵a
1=
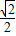
,n≥2,0<a
n+1<a
n<1
∴a
n<
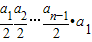
<
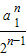
<
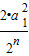
=
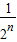
②.(14分)
由①②两式可知:b
n>a
n•n!.(16分)
点评:本题主要考查数列与函数,不等式的综合运用,主要涉及了数学归纳法,导数法,放缩法及累乘法等常用解题方法,综合性强,难度大,要求思路要清,意志力要强.

 ,bn+1≥
,bn+1≥ (n+1)bn,n∈N*.求证:
(n+1)bn,n∈N*.求证: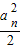
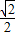 ,则当n≥2时,bn>an•n!.
,则当n≥2时,bn>an•n!. =
=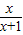 >0,所以f(x)在(0,1)上是增函数.可和f(0)<f(ak)<f(1),即0<ak+1<1<1-ln2<1.再由an+1-an=an-ln(1+an)-an=-ln(1+an)<0,有an+1<an.进而得到结论.
>0,所以f(x)在(0,1)上是增函数.可和f(0)<f(ak)<f(1),即0<ak+1<1<1-ln2<1.再由an+1-an=an-ln(1+an)-an=-ln(1+an)<0,有an+1<an.进而得到结论.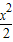 -f(x)=
-f(x)=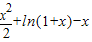 ,0<x<1,即证g(x)>0成立,用导数法研究因为g′(x)=
,0<x<1,即证g(x)>0成立,用导数法研究因为g′(x)=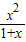 >0,知g(x)在(0,1)上增函数.得到结论.
>0,知g(x)在(0,1)上增函数.得到结论. ,bn+1≥
,bn+1≥ (n+1)bn,可再由bn>0,变形为
(n+1)bn,可再由bn>0,变形为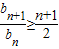 ,从而由累乘法可得bn=
,从而由累乘法可得bn=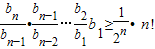 ①,再由an+1<
①,再由an+1<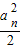 推知:
推知: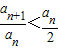 ,再用累乘法可得
,再用累乘法可得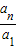 =
=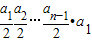 <
<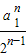 <
<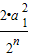 =
=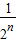 ②.由①②两式可得结论.
②.由①②两式可得结论.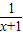 =
=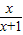 >0,
>0,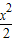 -f(x)=
-f(x)=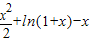 ,0<x<1,
,0<x<1,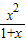 >0,知g(x)在(0,1)上增函数.
>0,知g(x)在(0,1)上增函数.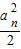 -f(an)>0,
-f(an)>0,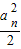 (10分)
(10分) ,bn+1≥
,bn+1≥ (n+1)bn,
(n+1)bn,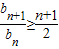 ,
,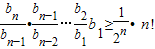 ①,(12分)
①,(12分)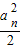 知:
知: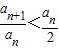 ,
,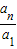 =
=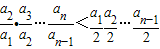 ,
,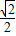 ,n≥2,0<an+1<an<1
,n≥2,0<an+1<an<1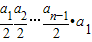 <
<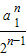 <
<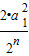 =
=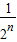 ②.(14分)
②.(14分)

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<