Question

【题目】如图，椭圆与一等轴双曲线相交，是其中一个交点，并且双曲线的顶点是该椭圆的焦点，，双曲线的焦点是椭圆的左、右顶点，设为该双曲线上异于顶点的任意一点，直线的斜率分别为，且直线和与椭圆的交点分别为、和、.

（1）求椭圆和双曲线的标准方程；

（2）（i）证明：；

（ii）是否存在常数，使得恒成立？若存在，求的值；若不存在，请说明理由.

Answer 1

【答案】（1），；(2）（i）证明见解析；（ii）存在，.

【解析】

（1）根据题意双曲线的，进而可求双曲线的标准方程；椭圆的，由可得，进而可得椭圆的标准方程.

（2）（i）设点，利用两点，，从而可得，将点代入双曲线方程即可证出；（ii）假设存在常数，使得恒成立，由（i）设直线的方程为，进而求出直线的方程，把直线代入椭圆方程，利用弦长公式求出， 同理求出弦长，代入整理即可求出的值

（1）由题意知，双曲线的，方程为：

椭圆：，即.

于是椭圆方程为；

（2）（i）设点，则，，

则；

而由点在双曲线上，可知，即有；

从而，故.

（ii）假设存在常数，使得恒成立.

则由（i）知，所以可设直线的方程为，

直线的方程为；

把直线的方程为代入椭圆方程，

整理得；

若设，，则有，；

因此；

同理可得；

因此由知

.

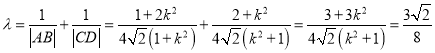所以存在常数，使得恒成立.