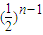Question

设C：y=x²（x＞0）上的点为P（x，y），在P处作曲线C的切线与x轴交于Q₁，过Q₁作平行于y轴的直线与曲线C交于P₁（x₁，y₁），然后在P₁作曲线C的切线与x轴交于Q₂，过Q₂作平行于y轴的直线与曲线C交于P₂（x₂，y₂），依此类推，作出以下各点：Q₃，P₃，…Q_n，P_n…．已知x=2，则数{x_n}的通项公式是    ．

Answer 1

【答案】分析：把x=2代入函数解析式，求出y的值，确定出P的坐标，求出函数解析式的导函数，把P的横坐标代入导函数中求出的导函数值为过P处作曲线C的切线的斜率，进而确定出切线的方程，令切线方程中y=0求出x的值，即为x₁的值，同理可求出x₂的值，依此类推，按照此规律即可表示出x_n的值，得出数列{x_n}的通项公式．
解答：解：∵x=2，P（x，y）在y=x²上，
∴y=2²=4，即P（2，4），
求导得：y′=2x，
∴在P处作曲线C的切线的斜率为y′_x=2=4，
则此切线方程为y-4=4（x-2），即y=4x-4，
令y=0，解得：x=1，即x₁=1，
∴P₁（1，1），
同理可得x₂=，x₃=，…，
∴x_n=．
故答案为：
点评：此题考查了等比数列的通项公式，曲线上过某点切线方程的斜率，一次函数与坐标轴的交点，直线的点斜式方程，是一道综合性较强的题型，锻炼了学生依此类推，归纳总结的能力．