
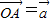 ,
,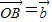 ,
,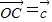 .
.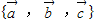 表示向量
表示向量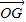 ;
;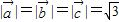 ,且
,且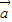 与
与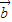 、
、 夹角的余弦值均为
夹角的余弦值均为 ,
, 与
与 夹角为60°,求
夹角为60°,求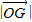 .
.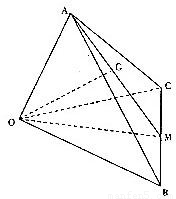
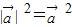 ,再将平方式展开结合向量的数量积求出其值即可.
,再将平方式展开结合向量的数量积求出其值即可. =
= (
(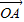
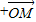 )
) =
= (
(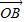
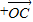 )
)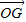 =
=
 +
+
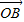 +
+
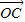 ,
,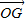 =
=
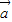
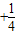
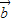 +
+
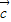
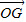 |2=(
|2=(
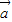 +
+
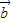 +
+
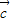 )2
)2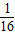 (4
(4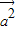 +
+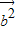
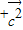 +4
+4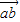 +4
+4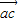 +2
+2 )
)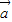 |=|
|=|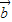 |=|
|=| |=
|=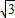 ,
,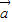 ,
,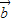 >=cos<
>=cos<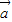 ,
,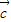 >=
>= ,cos<
,cos<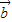 ,
,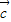 >=cos60°=
>=cos60°=
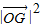 =
=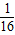 (4×3+3+3+4+4+3)=
(4×3+3+3+4+4+3)=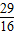
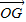 |=
|=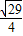 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:湖北随州曾都一中2008-2009学年高二下学期三月月考数学试题 题型:044
(理科作)如图,在空间四边形PACB中,O为AB的中点,PA=PB=![]() ,PA⊥PC,AB⊥BC,PO⊥平面ABC,∠BAC=30°.
,PA⊥PC,AB⊥BC,PO⊥平面ABC,∠BAC=30°.

(Ⅰ)求证:PA⊥PB;
(Ⅱ)求异面直线AB和PC所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁沈阳二中高二12月月考理科数学试卷(解析版) 题型:解答题
如图,在空间四边形SABC中,AC、BS为其对角线,O为△ABC的重心,

试证:(1) (;(2)
(;(2) .
.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试4 题型:解答题
|
 且
且
(Ⅰ)求k的值;
(Ⅱ)求
(文)某村计划建造一个室内面积为800m2的矩形蔬菜温室. 在温室内,种植蔬菜时需要沿左、右两侧与前侧内墙各保留1m宽的空地作为通道,后侧内墙不留空地(如图所示),问当温室的长是多少米时,能使蔬菜的种植面积最大?
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com