
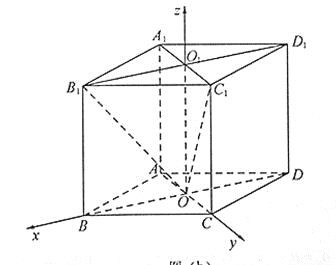
【题目】如图6,四棱柱![]() 的所有棱长都相等,
的所有棱长都相等,![]() ,四边形
,四边形![]() 和四边形
和四边形![]() 为矩形.
为矩形.
(1)证明:![]() 底面
底面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1) 详见解析 (2)![]()
【解析】
试题分析:(1)要证明线面垂直,只需要在面内找到两条相交的线段与之垂直即可,即证明![]() 与
与![]() 垂直,首先利用四棱柱所有棱相等,得到上下底面为菱形,进而得到
垂直,首先利用四棱柱所有棱相等,得到上下底面为菱形,进而得到![]() 均为中点,得到
均为中点,得到![]() 三者相互平行,四边形
三者相互平行,四边形![]() 均为矩形与平行相结合即可得到
均为矩形与平行相结合即可得到![]() 与
与![]() 垂直,进而证明线面垂直.
垂直,进而证明线面垂直.
(2)要求二面角,此问可以以以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立三维直角坐标系,利用空间向量的方法得到二面角的余弦值,在此说明第一种方法,做出二面角的平面角, 过
轴建立三维直角坐标系,利用空间向量的方法得到二面角的余弦值,在此说明第一种方法,做出二面角的平面角, 过![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,连接
,连接![]() .利用(1)得到
.利用(1)得到![]() ,在利用四边形
,在利用四边形![]() 为菱形,对角线相互垂直,两个垂直关系即可得到
为菱形,对角线相互垂直,两个垂直关系即可得到![]() 垂直于平面
垂直于平面![]() ,进而得到
,进而得到![]() ,结合
,结合![]() 得到线面垂直,说明角
得到线面垂直,说明角![]() 即为哦所求二面角的平面角,设四棱柱各边长为
即为哦所求二面角的平面角,设四棱柱各边长为![]() ,利用勾股定理求出相应边长即可得到角
,利用勾股定理求出相应边长即可得到角![]() 的余弦值,进而得到二面角的余弦值.
的余弦值,进而得到二面角的余弦值.
(1)证明:![]() 四棱柱
四棱柱![]() 的所有棱长都相等
的所有棱长都相等
![]() 四边形
四边形![]() 和四边形
和四边形![]() 均为菱形
均为菱形
![]()
![]()
![]()
![]() 分别为
分别为![]() 中点
中点
![]() 四边形
四边形![]() 和四边形
和四边形![]() 为矩形
为矩形
![]()
![]()
![]() 且
且![]()
![]()
又![]()
![]() 且
且![]() 底面
底面![]()
![]() 底面
底面![]() .
.
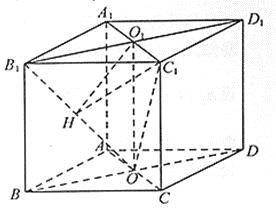
(2)法1::过![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,连接
,连接![]() .不妨设四棱柱
.不妨设四棱柱![]() 的边长为
的边长为![]() .
.
![]()
![]() 底面
底面![]() 且底面
且底面![]()
![]() 面
面![]()
![]() 面
面![]()
又![]() 面
面![]()
![]()
![]() 四边形
四边形![]() 为菱形
为菱形
![]()
又![]() 且
且![]() ,
,![]() 面
面![]()
![]() 面
面![]()
又![]() 面
面![]()
![]()
又![]() 且
且![]() ,
,![]() 面
面![]()
![]() 面
面![]()
![]()
![]() 为二面角
为二面角![]() 的平面角,则
的平面角,则![]()
![]() 且四边形
且四边形![]() 为菱形
为菱形
![]() ,
,![]()
![]() ,
,
则![]()
再由![]() 的勾股定理可得
的勾股定理可得![]() ,
,
则![]()
 ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.
法2:因为四棱柱![]() 的所有棱长都相等,所以四边形
的所有棱长都相等,所以四边形![]() 是菱形,因此
是菱形,因此![]() ,又
,又![]()
![]() 面
面![]() ,从而
,从而![]() 两两垂直,如图以
两两垂直,如图以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立三维直角坐标系,不妨设
轴建立三维直角坐标系,不妨设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,于是各点的坐标为:
,于是各点的坐标为:![]() ,已知
,已知![]() 是平面
是平面![]() 的一个法向量,设
的一个法向量,设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则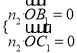 ,
,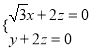 ,取
,取![]() ,则
,则![]() ,
,
所以![]() ,
,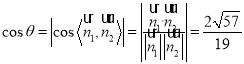 ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2015年推出一种新型家用轿车,购买时费用为16.9万元,每年应交付保险费、养路费及汽油费共1.2万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O:![]() 和点
和点![]() ,由圆O外一点P向圆O引切线
,由圆O外一点P向圆O引切线![]() ,Q为切点,且有
,Q为切点,且有![]() .
.
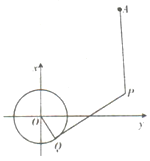
(1)求点P的轨迹方程,并说明点P的轨迹是什么样的几何图形?
(2)求![]() 的最小值;
的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大小相同的小球![]() 个,在小球上分别标有1,2,3…,
个,在小球上分别标有1,2,3…,![]() 的号码,已知从盒子中随机取出两个球,两球号码的最大值为
的号码,已知从盒子中随机取出两个球,两球号码的最大值为![]() 的概率为
的概率为![]() .
.
(Ⅰ)盒子中装有几个小球?
(Ⅱ)现从盒子中随机地取出4个球,记所取4个球的号码中,连续自然数的个数的最大值为随机变量![]() (如取标号分别为2,4,6,8的小球时
(如取标号分别为2,4,6,8的小球时![]() ;取标号分别为1,2,4,6的小球时
;取标号分别为1,2,4,6的小球时![]() ;取标号分别为1,2,3,5的小球时
;取标号分别为1,2,3,5的小球时![]() ),求
),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是0.7.现采用随机模拟的方法估计该运动员射击4次,至少击中2次的概率:先由计算器算出0~9之间取整数值的随机数,指定0,1,2表示没有击中目标,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
据此估计,该射击运动员射击4次至少击中2次的概率为( )
A. 0.8 B. 0.85 C. 0.9 D. 0.95
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com