
思路分析:输入三个实数a,b,c,先判断a是否为零,若不为零,则通过判断判别式来求实根.
程序框图如图1-2-12所示.
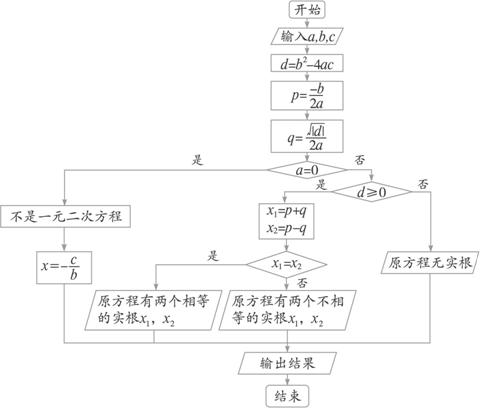
图1-2-12
程序步骤如下:
input a,b,c
d=b^2-4*a*c;
p=-b/(2*a);
q=sqrt(ABS(d))/(2*a);
if a=0
print(%io(2),“yuan fang cheng bu shi yi yuan er ci fang cheng”);
x=-c/b;
print(%io(2),x);
else
if d>=0
x1=p+q;
x2=p-q;
print(%io(2),x1,x2);
else
print(%io(2),“yuan fang cheng wu shi gen”);
end
end
点评:①当a=0时,输出“不是一元二次方程”;②当b2-4ac>0时,求得并输出两个不相等实根;③当b2-4ac=0时,求得并输出两个相等实根;④当b2-4ac<0时,输出“无实数根”.由于需要分情况讨论,故采用条件结构画出流程图,应用条件语句写出程序.本例在前例的基础上加了条件,需要判断a是否为零.例6、例7这两个题放在一起对于锻炼我们的思维能力很有好处,两个题目的巧妙之处在于一个告诉了是一元二次方程,而另一个需要判断是否为一元二次方程,这一点正是我们容易忽略的地方.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| n |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市邛崃市高三(上)12月统考数学试卷(理科)(解析版) 题型:解答题
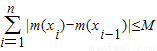 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: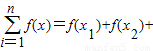 …+f(xn))
…+f(xn))查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省烟台市牟平区高三(上)模块检测数学试卷(理科)(解析版) 题型:解答题
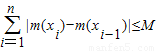 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: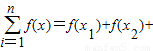 …+f(xn))
…+f(xn))查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com