
(本小题共14分)
数列 的前n项和为
的前n项和为 ,点
,点 在直线
在直线
上.
(I)求证:数列 是等差数列;
是等差数列;
(II)若数列 满足
满足 ,求数列
,求数列 的前n项和
的前n项和
(III)设 ,求证:
,求证:
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源:2011-2012学年北京市东城区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数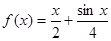 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
,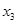 ,当
,当 ,且
,且 时,
时, .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市东城区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题共14分)已知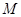 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意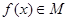 ,①方程
,①方程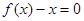 有实数根;②函数
有实数根;②函数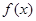 的导数
的导数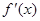 满足
满足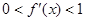 .
.
(Ⅰ)判断函数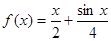 是否是集合
是否是集合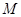 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合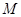 中的元素
中的元素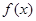 具有下面的性质:若
具有下面的性质:若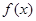 的定义域为
的定义域为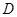 ,则对于任意
,则对于任意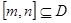 ,都存在
,都存在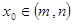 ,使得等式
,使得等式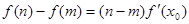 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程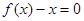 有且只有一个实数根;
有且只有一个实数根;
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市房山区高三统练数学理卷 题型:解答题
(本小题共14分)
设函数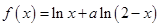 .
.
(Ⅰ)求函数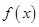 的定义域及其导数
的定义域及其导数 ;
;
(Ⅱ)当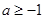 时,求函数
时,求函数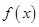 的单调区间;
的单调区间;
(Ⅲ)当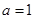 时,令
时,令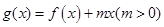 ,若
,若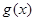 在
在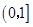 上的最大值为
上的最大值为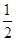 ,求实数
,求实数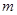 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
(本小题共14分) 设函数. (Ⅰ)求函数的定义域及其导数; (Ⅱ)当时,求函数的单调区间; (Ⅲ)当时,令,若在上的最大值为,求实数的值. 查看答案和解析>> 科目:高中数学 来源: 题型: (2010北京理数)(19)(本小题共14分) 在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于 (Ⅰ)求动点P的轨迹方程; (Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |