
【题目】如图,椭圆![]() :
:![]() 与圆
与圆![]() :
:![]() 相切,并且椭圆
相切,并且椭圆![]() 上动点与圆
上动点与圆![]() 上动点间距离最大值为
上动点间距离最大值为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,
,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 面积的最大值,并求取得最大值时直线
面积的最大值,并求取得最大值时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)面积的最大值为
;(2)面积的最大值为![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
【解析】
(1)由题意可得b=1,a﹣1![]() ,即可得到椭圆的方程;(2)设A(x1,y1),B(x2,y2),根据l2⊥l1,可设直线l1,l2的方程,分别与椭圆、圆的方程联立即可得可得出|AB|、|MN|,即可得到三角形ABC的面积,利用基本不等式的性质即可得出其最大值.
,即可得到椭圆的方程;(2)设A(x1,y1),B(x2,y2),根据l2⊥l1,可设直线l1,l2的方程,分别与椭圆、圆的方程联立即可得可得出|AB|、|MN|,即可得到三角形ABC的面积,利用基本不等式的性质即可得出其最大值.
(1)椭圆E与圆O:x2+y2=1相切,知b2=1;
又椭圆E上动点与圆O上动点间距离最大值为![]() ,即椭圆中心O到椭圆最远距离为
,即椭圆中心O到椭圆最远距离为![]() ,
,
得椭圆长半轴长![]() ,即
,即![]() ;
;
所以椭圆E的方程:![]()
(2)①当l1与x轴重合时,l2与圆相切,不合题意.
②当l1⊥x轴时,M(﹣1,0),l1:x=1,![]() ,此时
,此时![]() .…(6分)
.…(6分)
③当l1的斜率存在且不为0时,设l1:x=my+1,m≠0,则![]() ,
,
设A(x1,y1),B(x2,y2),由 得,(2m2+3)y2+4my﹣1=0,
得,(2m2+3)y2+4my﹣1=0,
所以![]() ,
,
所以![]() .
.
由 得,
得,![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以![]()
 , 因为
, 因为![]() ,
,
![]() 所以
所以![]() ,
,
当且仅当![]() 时取等号.所以
时取等号.所以![]() (
(![]() )
)
综上,△ABM面积的最大值为![]() ,此时直线l1的方程为
,此时直线l1的方程为![]() .
. 


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】某运输公司有![]() 名驾驶员和
名驾驶员和![]() 名工人,有
名工人,有![]() 辆载重量为
辆载重量为![]() 吨的甲型卡车和
吨的甲型卡车和![]() 辆载重量为
辆载重量为![]() 吨的乙型卡车.某天需运往
吨的乙型卡车.某天需运往![]() 地至少
地至少![]() 吨的货物,派用的车需满载且只运送一次.派用的每辆甲型卡车需配
吨的货物,派用的车需满载且只运送一次.派用的每辆甲型卡车需配![]() 名工人,运送一次可得利润
名工人,运送一次可得利润![]() 元:派用的每辆乙型卡车需配
元:派用的每辆乙型卡车需配![]() 名工人,运送一次可得利润
名工人,运送一次可得利润![]() 元,该公司合理计划当天派用两类卡车的车辆数,可得的最大利润多少?
元,该公司合理计划当天派用两类卡车的车辆数,可得的最大利润多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)该种植基地在如图所示的长方形地块的每个格点(横纵直线的交点)处都种了一株该种水果,其中每个小正方形的面积都为![]() ,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
,现从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的平均数.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“若![]() ,则x,y互为倒数”的逆命题;
,则x,y互为倒数”的逆命题;
②“面积相等的三角形全等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“若![]() ,则
,则![]() ”的逆命题。
”的逆命题。
其中真命题是( )
A.①②④B.②③④C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)>3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
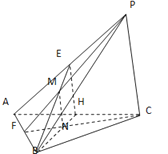
【题目】如图,在三棱锥![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,E、F、H分别为AP、AB、AC的中点,PF交BE于点M,CF交BH于点N,
,E、F、H分别为AP、AB、AC的中点,PF交BE于点M,CF交BH于点N,![]() ,
,![]() .
.
![]() 求证:
求证:![]() 平面BEH;
平面BEH;
![]() 求证:
求证:![]() ;
;
![]() 求直线PA与平面ABC所成角的正弦值.
求直线PA与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着计算机的出现,图标被赋予了新的含义,又有了新的用武之地.在计算机应用领域,图标成了具有明确指代含义的计算机图形.如图所示的图标是一种被称之为“黑白太阳”的图标,该图标共分为3部分.第一部分为外部的八个全等的矩形,每一个矩形的长为3、宽为1;第二部分为圆环部分,大圆半径为3,小圆半径为2;第三部分为圆环内部的白色区域.在整个“黑白太阳”图标中随机取一点,则此点取自图标第三部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程是:
的极坐标方程是:![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程.
的直角坐标方程.
(2)点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值与最小值.
距离的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com