
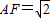 .
.
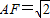 .可求得AC=2
.可求得AC=2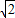 ,即CO=AO=AF=CE=
,即CO=AO=AF=CE=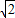 ,由于三角形ECO与三角形FAO都是直角三角形,故可得∠EOC=∠FOA=45°,所以∠EOF=90°,即EO⊥OF
,由于三角形ECO与三角形FAO都是直角三角形,故可得∠EOC=∠FOA=45°,所以∠EOF=90°,即EO⊥OF 过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,
过O作OP⊥AD于P,过P作PM⊥DF于M,连接OM,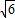 ,由P是中点得DP=1,
,由P是中点得DP=1, 得MP=
得MP=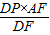 =
=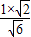 =
=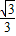
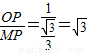


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,CD=2AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,直线AB的方程为6x-3y-4=0,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,则飞镖落在阴影部分(三角形ABC的内部)的概率是( )
如图所示,直线AB的方程为6x-3y-4=0,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,则飞镖落在阴影部分(三角形ABC的内部)的概率是( )查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•金华模拟)如图所示的正方形中,将边AB、AD各4等分,分别作AB、AD的平行线段成4×4方格网,则从图中取出一由网格线形成的矩形,恰好为正方形的概率是
(2012•金华模拟)如图所示的正方形中,将边AB、AD各4等分,分别作AB、AD的平行线段成4×4方格网,则从图中取出一由网格线形成的矩形,恰好为正方形的概率是| 3 |
| 10 |
| 3 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com