
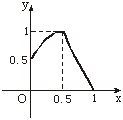
其中f1(x)=-2(x-![]() )2+1,f2(x)=-2x+2.
)2+1,f2(x)=-2x+2.
(Ⅰ)在下面坐标系上画出y=f(x)的图象;
(Ⅱ)设y=f2(x)(x![]() [
[![]() ])的反函数为y=g(x),a1=1,a2=g(a1),…,an=g(an-1);
])的反函数为y=g(x),a1=1,a2=g(a1),…,an=g(an-1);
求数列{an}的通项公式,并求![]() ;
;
(Ⅲ)若x0![]() [0,
[0,![]() ),x1=f(x0),f(x1)=x0,求x0.
),x1=f(x0),f(x1)=x0,求x0.
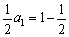
24.本小题主要考查函数及数列的基本概念和性质,考查分析、归纳、推理、运算的能力.
解:
(Ⅰ)函数图象:
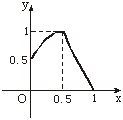
说明:图象过(0,![]() )、(
)、(![]() ,1)、(1,0)点;在区间[0,
,1)、(1,0)点;在区间[0, ![]() )上的图象为上凸的曲线段;在区间[
)上的图象为上凸的曲线段;在区间[![]() ,1]上的图象为直线段.
,1]上的图象为直线段.
(Ⅱ)f2(x)=-2x+2,x∈[![]() ,1]的反函数为:y=1-
,1]的反函数为:y=1-![]() ,x∈[0,1].
,x∈[0,1].
由已知条件得:
a1=1,
a2=1-![]() ,
,
a3=1-![]() ,
,
a4=1+(![]() )1+
)1+![]() ,
,
……
∴![]() =
=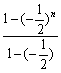 ,
,
即 ![]() ,
,
∴![]() .
.
(Ⅲ)由已知x0∈[0,![]() ),
),
∴x1=f1(x0)=1-2(x0-![]() )2.
)2.
由f1(x)的值域,得x1∈[![]() ],
],
∴f2(x1)=2-2[1-2(x0-![]() )2]=4(x0-
)2]=4(x0-![]() )2.
)2.
由f2(x1)=x0,整理得 ![]() ,
,
解得 x0=1或x0=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com