
已知常数 、
、 、
、 都是实数,函数
都是实数,函数 的导函数为
的导函数为 ,
, 的解集为
的解集为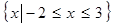 .
.
(Ⅰ)若 的极大值等于
的极大值等于 ,求
,求 的极小值;
的极小值;
(Ⅱ)设不等式 的解集为集合
的解集为集合 ,当
,当 时,函数
时,函数 只有一个零点,求实数
只有一个零点,求实数 的取值范围.
的取值范围.
(Ⅰ)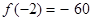 ;(Ⅱ)当
;(Ⅱ)当 或
或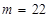 时,函数
时,函数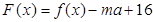 在
在 上只有一个零点.
上只有一个零点.
【解析】
试题分析::1.第(Ⅰ)的解答还是要破费周折的.首先要求出导函数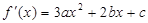 .
.
然后根据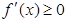 的解集为
的解集为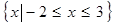 ,通过解混合组,得到
,通过解混合组,得到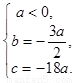 进而得到
进而得到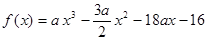 .接下来通过研究函数
.接下来通过研究函数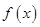 的单调性,由
的单调性,由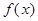 的极大值等于
的极大值等于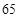 ,可解得
,可解得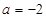 ,这样就可以求出
,这样就可以求出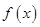 的极小值
的极小值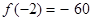 .2.第(Ⅱ)问先由不等式
.2.第(Ⅱ)问先由不等式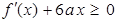 的解集为集合
的解集为集合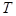 ,可以解得
,可以解得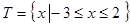 .然后研究
.然后研究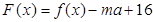 的单调性,值得注意的是
的单调性,值得注意的是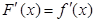 ,换句话说方程两边对
,换句话说方程两边对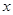 求导数,
求导数, 、
、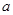 应看作是常数.单调性弄清楚后,还要比较
应看作是常数.单调性弄清楚后,还要比较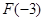 、
、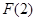 的大小.然后根据
的大小.然后根据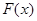 只有一个零点,列出
只有一个零点,列出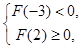 或
或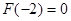 ,最后解之即可.值得注意的是,很多考生漏了
,最后解之即可.值得注意的是,很多考生漏了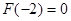 .
.
试题解析:(Ⅰ)∵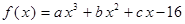 ,∴
,∴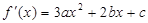 .
.
∵不等式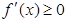 的解集为
的解集为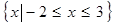 ,
,
∴不等式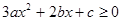 的解集为
的解集为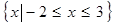 .
.
∴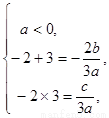 即
即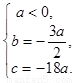
∴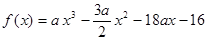 ,
,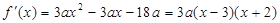 .
.
∴当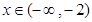 或
或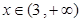 时,
时,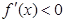 ,即
,即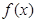 为单调递减函数;
为单调递减函数;
当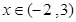 时,
时, ,即
,即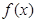 为单调递增函数.
为单调递增函数.
∴当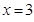 时,
时,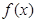 取得极大值,当
取得极大值,当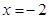 时,
时,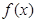 取得极小值.
取得极小值.
由已知得 ,解得
,解得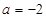 .
.
∴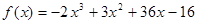 .
.
∴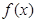 的极小值
的极小值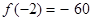 .
.
(Ⅱ)∵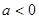 ,
, ,
,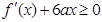 ,
,
∴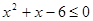 ,解得
,解得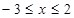 ,即
,即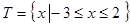 .
.
∵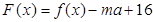 ,∴
,∴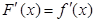 .
.
∴当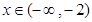 或
或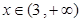 时,
时,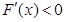 ,即
,即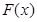 为单调递减函数;
为单调递减函数;
当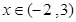 时,
时, ,即
,即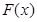 为单调递增函数.
为单调递增函数.
∴当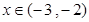 时,
时,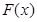 为单调递减函数;
为单调递减函数;
当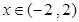 时,
时,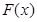 为单调递增函数.
为单调递增函数.
∵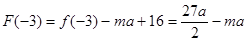 ,
,
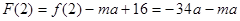 ,
,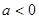 ,
,
∴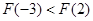 .
.
∴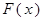 在
在 上只有一个零点
上只有一个零点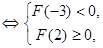 或
或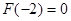 .
.
由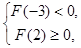 得
得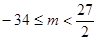 ;
;
由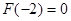 ,即
,即 ,得
,得 .
.
∴实数 的取值范围为
的取值范围为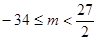 或
或 .
.
∴当 或
或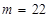 时,函数
时,函数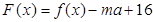 在
在 上只有一个零点.
上只有一个零点.
考点:本题通过导数综合考查函数的单调性、极值、零点、比较大小等知识.


科目:高中数学 来源:2012-2013学年云南省毕业生复习第二次统一检测理科数学试卷(解析版) 题型:选择题
已知常数 、
、 、
、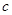 都是实数,
都是实数, 的导函数为
的导函数为 ,
, 的解集为
的解集为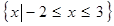 ,若
,若 的极小值等于
的极小值等于 ,则
,则 的值是( )
的值是( )
(A) (B)
(B)
(C) (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com