
(本小题12分) a,b,c为△ABC的三边,其面积S△ABC=12 ,bc=48,b-c=2,求a;
,bc=48,b-c=2,求a;
当A=60°时,a2=52,a=2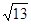 ,当A=120°时,a2=148,a=2
,当A=120°时,a2=148,a=2 。
。
【解析】
试题分析:利用三角形的面积公式列出关于sinA的等式,求出sinA的值,通过解已知条件中关于b,c的方程求出b,c的值,分两种情况,利用余弦定理求出边a的值.
解:由S△ABC=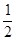 bcsinA,得12
bcsinA,得12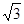 =
=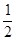 ×48×sinA
×48×sinA
∴ sinA=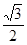 2分
2分
∴ A=60°或A=120° 2分
a2=b2+c2-2bccosA
=(b-c)2+2bc(1-cosA)
=4+2×48×(1-cosA) 4分
当A=60°时,a2=52,a=2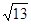 2分
2分
当A=120°时,a2=148,a=2 2分
2分
考点:本题主要考查运用正弦面积公式和余弦定理解三角形问题。
点评:解决该试题的关键是求三角形的题目,一般利用正弦定理、余弦定理及三角形的面积公式列方程解决


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源:2014届福建福州文博中学高二上学期期中考试数学试卷(解析版) 题型:解答题
(本小题12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(1)求角C的大小;
(2)若c= ,且△ABC的面积为
,且△ABC的面积为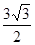
 ,求a+b的值。
,求a+b的值。
查看答案和解析>>
科目:高中数学 来源:2014届福建省福州外国语学校高二上学期期中考试数学试卷(解析版) 题型:解答题
(本小题12分)ΔABC中A,B,C的对边分别为a,b,c,且
求:(1)角B的大小; (2)若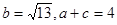 ,求ΔABC的面积.
,求ΔABC的面积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省常德市高三质量检测考试数学理卷 题型:解答题
(本小题12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为 ,服用B有效的概率为
,服用B有效的概率为 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ) 观察3个试验组,用 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源:2014届江西省上饶市高一下学期第一次月考数学 题型:解答题
(本小题12分)已知a,b,c分别是△ABC的三个内角A、B、C的对边.
(Ⅰ)若△ABC面积为 求a,b的值;
求a,b的值;
(Ⅱ)若acosa=bcosB,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为![]() ,服用B有效的概率为
,服用B有效的概率为![]() 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ) 观察3个试验组,用![]() 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com