
已知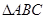 中,角
中,角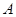 ,
,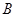 ,
,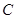 所对的边分别为
所对的边分别为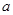 ,
,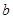 ,
,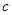 ,外接圆半径是
,外接圆半径是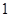 ,,且满足条件
,,且满足条件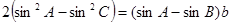 ,则
,则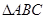 的面积的最大值为 (
)
的面积的最大值为 (
)
A.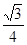 B.
B.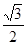 C.
C.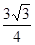 D.
D.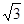
C
【解析】
试题分析:由正弦定理可得b=2RsinB=2sinB,代入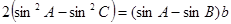 得 2sin2A-2sin2C=2sinAsinB-2sin2B,所以sin2A+sin2B-sin2C=sinAsinB,
得 2sin2A-2sin2C=2sinAsinB-2sin2B,所以sin2A+sin2B-sin2C=sinAsinB,
又由正弦定理得:a2+b2-c2=ab,∴cosC=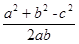
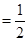 ,又C为三角形的内角,所以C=60°.
,又C为三角形的内角,所以C=60°.
因为ab=a2+b2-c2=a2+b2-(2rsinC)2=a2+b2-3≥2ab-3,所以ab≤3 (当且仅当a=b时,取等号),
所以△ABC面积为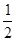 absinC≤
absinC≤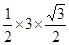 =
= 。
。
考点:本题考查正弦定理;余弦定理;三角形的面积公式;三角函数中的恒等变换;基本不等式的应用。
点评:本题的主要思路是:由ab=a2+b2-3≥2ab-3
求得ab最大值为3,从而求得△ABC面积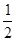 absinC 的最大值.其中求出ab≤3是解题的难点.
absinC 的最大值.其中求出ab≤3是解题的难点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年广东省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
已知 中,三条边
中,三条边 所对的角分别为
所对的角分别为 、
、 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市高三毕业班质量检查理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
已知 分别在射线
分别在射线 (不含端点
(不含端点 )上运动,
)上运动, ,在
,在 中,角
中,角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 .
.

(Ⅰ)若 、
、 、
、 依次成等差数列,且公差为2.求
依次成等差数列,且公差为2.求 的值;
的值;
(Ⅱ)若 ,
, ,试用
,试用 表示
表示 的周长,并求周长的最大值.
的周长,并求周长的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省长葛市高三上学期期中考试数学理卷 题型:解答题
(本小题12分)已知 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、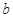 、
、 ,且
,且 。
。
(I)求 的值;
的值;
(II)若 的面积
的面积 ,且
,且 ,求
,求 的外接圆半径
的外接圆半径 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com