
已知等差数列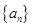 前三项的和为
前三项的和为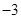 ,前三项的积为
,前三项的积为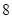 。
。
(1) 求等差数列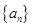 的通项公式;
的通项公式;
(2)若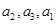 成等比数列,求数列
成等比数列,求数列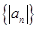 的前
的前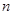 项和
项和
(1)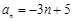 ,或
,或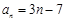 .
.
(2)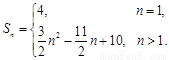
【解析】考察等差等比数列的通项公式,和前n项和公式及基本运算。
(Ⅰ)设等差数列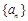 的公差为
的公差为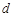 ,则
,则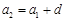 ,
,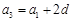 ,
,
由题意得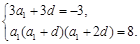 解得
解得 或
或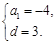
所以由等差数列通项公式可得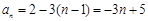 ,或
,或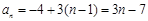 .
.
故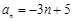 ,或
,或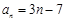 .
.
(Ⅱ)当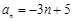 时,
时,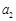 ,
,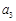 ,
,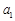 分别为
分别为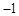 ,
, ,
,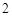 ,不成等比数列;
,不成等比数列;
当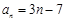 时,
时,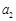 ,
,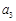 ,
,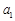 分别为
分别为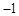 ,
,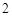 ,
, ,成等比数列,满足条件.
,成等比数列,满足条件.
故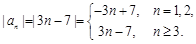
记数列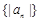 的前
的前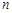 项和为
项和为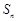 .
.
当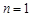 时,
时,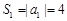 ;当
;当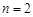 时,
时,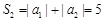 ;
;
当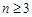 时,
时,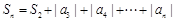
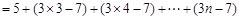
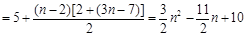 . 当
. 当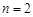 时,满足此式.
时,满足此式.
综上,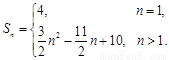
【点评】本题考查等差数列的通项,求和,分段函数的应用等;考查分类讨论的数学思想以及运算求解的能力.求等差数列的通项一般利用通项公式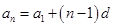 求解;有时需要利用等差数列的定义:
求解;有时需要利用等差数列的定义: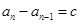 (
( 为常数)或等比数列的定义:
为常数)或等比数列的定义: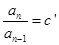 (
(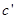 为常数,
为常数,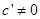 )来判断该数列是等差数列或等比数列,然后再求解通项;有些数列本身不是等差数列或等比数列,但它含有无数项却是等差数列或等比数列,这时求通项或求和都需要分段讨论.来年需注意等差数列或等比数列的简单递推或等差中项、等比中项的性质.
)来判断该数列是等差数列或等比数列,然后再求解通项;有些数列本身不是等差数列或等比数列,但它含有无数项却是等差数列或等比数列,这时求通项或求和都需要分段讨论.来年需注意等差数列或等比数列的简单递推或等差中项、等比中项的性质.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山西省高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知等差数列 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为 .
.
(1)求等差数列 的通项公式;
的通项公式;
(2)若 ,
, ,
, 成等比数列,求数列
成等比数列,求数列 的前
的前 项和.
项和.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省高三下学期5月月考理科数学试卷(解析版) 题型:解答题
已知等差数列 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为 .
.
(Ⅰ)求等差数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
, 成等比数列,求数列
成等比数列,求数列 的前
的前 项和.
项和.
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖北卷解析版) 题型:解答题
(本小题满分12分)
已知等差数列 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为 .
.
(Ⅰ)求等差数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,
, 成等比数列,求数列
成等比数列,求数列 的前
的前 项和
项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com