
. (满分12分)
矩形ABCD的对角线AC、BD相交于点M (2,0),AB边所在直线的方程为: .
.
若点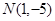 在直线AD上.
在直线AD上.
(1)求点A的坐标及矩形ABCD外接圆的方程;
(2)过直线 上一点P作(1)中所求圆的切线,设切点为E、F,求四边形PEMF面积的最小值,并求此时
上一点P作(1)中所求圆的切线,设切点为E、F,求四边形PEMF面积的最小值,并求此时 的值.
的值.
(1)∵AC⊥AD 且 ∴
∴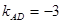
∴直线AD的方程为:y+5=-3(x-1) 即3x+y+2=0
由 解得
解得 即A(0,-2)
即A(0,-2)
∵ABCD是矩形 ∴ABCD外接圆的圆心为对角线AC与BD的交点,即M(2,0),
半径r=|AM|=2. 故其方程为
(2)由切线的性质知:四边形PEMF的面积S=|PE|•r=r
=
∴四边形PEMF的面积取最小值时,|PM|最小,即为圆心M到直线x-y+4=0的距离d=3.
∴四边形PEMF的面积S的最小值
此时||=||=,设∠MPE=∠MPF=α , 则
∴ =||2cos2=||2
(1-2sin2)=10[1-2()2]=
=||2cos2=||2
(1-2sin2)=10[1-2()2]=
【解析】略


科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
在一次篮球练习课中,规定每人最多投篮5次,若投中2次就称为“通过”,若投中3次就称为“优秀”并停止投篮.已知甲每次投篮投中的概率是![]() .
.
(I)求甲恰好投篮3次就通过的概率;
(II)设甲投篮投中的次数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望E
的分布列及数学期望E![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com