
ЁОЬтФПЁПФГЫЎЙћжжжВЛљЕив§НјвЛжжаТЫЎЙћЦЗжжЃЌОбаОПЗЂЯжИУЫЎЙћУПжъЕФВњСП![]() ЃЈЕЅЮЛЃК
ЃЈЕЅЮЛЃК![]() ЃЉКЭгыЫќЁАЯрНќЁБЕФжъЪ§
ЃЉКЭгыЫќЁАЯрНќЁБЕФжъЪ§![]() ОпгаЯпадЯрЙиЙиЯЕЃЈСНжъзїЮяЁАЯрНќЁБЪЧжИЫќУЧЕФжБЯпОрРыВЛГЌЙ§
ОпгаЯпадЯрЙиЙиЯЕЃЈСНжъзїЮяЁАЯрНќЁБЪЧжИЫќУЧЕФжБЯпОрРыВЛГЌЙ§![]() ЃЉЃЌВЂЗжБ№МЧТМСЫЯрНќжъЪ§ЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЪБУПжъВњСПЕФЯрЙиЪ§ОнШчЯТЃК
ЃЉЃЌВЂЗжБ№МЧТМСЫЯрНќжъЪ§ЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЪБУПжъВњСПЕФЯрЙиЪ§ОнШчЯТЃК
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
ЃЈ1ЃЉЧѓГіИУжжЫЎЙћУПжъЕФВњСП![]() ЙигкЫќЁАЯрНќЁБжъЪ§
ЙигкЫќЁАЯрНќЁБжъЪ§![]() ЕФЛиЙщЗНГЬЃЛ
ЕФЛиЙщЗНГЬЃЛ
ЃЈ2ЃЉИУжжжВЛљЕидкШчЭМЫљЪОЕФГЄЗНаЮЕиПщЕФУПИіИёЕуЃЈКсзнжБЯпЕФНЛЕуЃЉДІЖМжжСЫвЛжъИУжжЫЎЙћЃЌЦфжаУПИіаЁе§ЗНаЮЕФУцЛ§ЖМЮЊ![]() ЃЌЯжДгЫљжжЕФИУЫЎЙћжаЫцЛњбЁШЁвЛжъЃЌЪдИљОнЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌдЄВтЫќЕФВњСПЕФЦНОљЪ§.
ЃЌЯжДгЫљжжЕФИУЫЎЙћжаЫцЛњбЁШЁвЛжъЃЌЪдИљОнЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌдЄВтЫќЕФВњСПЕФЦНОљЪ§.
ИНЃКЛиЙщЗНГЬ![]() жааБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК
жааБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК ЃЌ
ЃЌ![]() .
.


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧвгы
ЃЌЧвгы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() СНЕу.
СНЕу.
ЃЈ1ЃЉЧѓдВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрНЛЃЌЧѓЪЕЪ§
ЯрНЛЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЪдЬжТлжБЯп![]() гыЃЈ1ЃЉаЁЬтЫљЧѓдВ
гыЃЈ1ЃЉаЁЬтЫљЧѓдВ![]() ЕФНЛЕуИіЪ§.
ЕФНЛЕуИіЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНЬхABCDЉA1B1C1D1жаЃЌРтГЄЮЊ2ЃЌMЃЌNЗжБ№ЮЊA1BЃЌACЕФжаЕуЃЎ
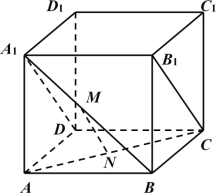
ЃЈ1ЃЉжЄУїЃКMN//B1CЃЛ
ЃЈ2ЃЉЧѓA1BгыЦНУцA1B1CDЫљГЩНЧЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
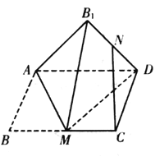
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌНЋ
ЕФжаЕуЃЌНЋ![]() бижБЯп
бижБЯп![]() ЗелГЩ
ЗелГЩ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌдђдкЗелЙ§ГЬжаЃЌЯТСаЫЕЗЈжаЫљгае§ШЗЕФађКХЪЧ_______.
ЕФжаЕуЃЌдђдкЗелЙ§ГЬжаЃЌЯТСаЫЕЗЈжаЫљгае§ШЗЕФађКХЪЧ_______.
ЂйДцдкФГИіЮЛжУЃЌЪЙЕУ![]() ЃЛ
ЃЛ
ЂкЗелЙ§ГЬжаЃЌ![]() ЕФГЄЪЧЖЈжЕЃЛ
ЕФГЄЪЧЖЈжЕЃЛ
ЂлШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂмШє![]() ЃЌЕБШ§РтзЖ
ЃЌЕБШ§РтзЖ![]() ЕФЬхЛ§зюДѓЪБЃЌШ§РтзЖ
ЕФЬхЛ§зюДѓЪБЃЌШ§РтзЖ![]() ЕФЭтНгЧђЕФБэУцЛ§ЪЧ
ЕФЭтНгЧђЕФБэУцЛ§ЪЧ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћжжжВЛљЕив§НјвЛжжаТЫЎЙћЦЗжжЃЌОбаОПЗЂЯжИУЫЎЙћУПжъЕФВњСП![]() ЃЈЕЅЮЛЃК
ЃЈЕЅЮЛЃК![]() ЃЉКЭгыЫќЁАЯрНќЁБЕФжъЪ§
ЃЉКЭгыЫќЁАЯрНќЁБЕФжъЪ§![]() ОпгаЯпадЯрЙиЙиЯЕЃЈСНжъзїЮяЁАЯрНќЁБЪЧжИЫќУЧЕФжБЯпОрРыВЛГЌЙ§
ОпгаЯпадЯрЙиЙиЯЕЃЈСНжъзїЮяЁАЯрНќЁБЪЧжИЫќУЧЕФжБЯпОрРыВЛГЌЙ§![]() ЃЉЃЌВЂЗжБ№МЧТМСЫЯрНќжъЪ§ЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЪБУПжъВњСПЕФЯрЙиЪ§ОнШчЯТЃК
ЃЉЃЌВЂЗжБ№МЧТМСЫЯрНќжъЪ§ЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌ4ЪБУПжъВњСПЕФЯрЙиЪ§ОнШчЯТЃК
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
ЃЈ1ЃЉЧѓГіИУжжЫЎЙћУПжъЕФВњСП![]() ЙигкЫќЁАЯрНќЁБжъЪ§
ЙигкЫќЁАЯрНќЁБжъЪ§![]() ЕФЛиЙщЗНГЬЃЛ
ЕФЛиЙщЗНГЬЃЛ
ЃЈ2ЃЉгавЛжжжВЛЇзМБИжжжВИУжжЫЎЙћ500жъЃЌЧвУПжъгыЫќЁАЯрНќЁБЕФжъЪ§ЖМЮЊ![]() ЃЌМЦЛЎЪеЛёКѓФмШЋВПЪлГіЃЌМлИёЮЊ10дЊ
ЃЌМЦЛЎЪеЛёКѓФмШЋВПЪлГіЃЌМлИёЮЊ10дЊ![]() ЃЌШчЙћЪеШыЃЈЪеШы=ВњСПЁСМлИёЃЉВЛЕЭгк25000дЊЃЌдђ
ЃЌШчЙћЪеШыЃЈЪеШы=ВњСПЁСМлИёЃЉВЛЕЭгк25000дЊЃЌдђ![]() ЕФзюДѓжЕЪЧЖрЩйЃП
ЕФзюДѓжЕЪЧЖрЩйЃП
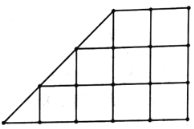
ЃЈ3ЃЉИУжжжВЛљЕидкШчЭМЫљЪОЕФжБНЧЬнаЮЕиПщЕФУПИіНЛВцЕуЃЈжБЯпЕФНЛЕуЃЉДІЖМжжСЫвЛжъИУжжЫЎЙћЃЌЦфжаУПИіаЁе§ЗНаЮЕФБпГЄКЭжБНЧШ§НЧаЮЕФжБНЧБпГЄЖМЮЊ![]() ЃЌвбжЊИУЬнаЮЕиПщжмБпЮоЦфЫћЪїФОгАЯьЃЌШєДгЫљжжЕФИУЫЎЙћжаЫцЛњбЁШЁвЛжъЃЌЪдИљОнЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌдЄВтЫќЕФВњСПЕФЗжВМСагыЪ§бЇЦкЭћ.
ЃЌвбжЊИУЬнаЮЕиПщжмБпЮоЦфЫћЪїФОгАЯьЃЌШєДгЫљжжЕФИУЫЎЙћжаЫцЛњбЁШЁвЛжъЃЌЪдИљОнЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌдЄВтЫќЕФВњСПЕФЗжВМСагыЪ§бЇЦкЭћ.
ИНЃКЛиЙщЗНГЬ![]() жааБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК
жааБТЪКЭНиОрЕФзюаЁЖўГЫЗЈЙРМЦЙЋЪНЗжБ№ЮЊЃК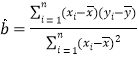 ЃЌ
ЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉвбжЊдВ![]() Й§Еу
Й§Еу![]() ЃЌЧвгыжБЯп
ЃЌЧвгыжБЯп![]() ЯрЧагкЕу
ЯрЧагкЕу![]() ЃЌЧѓдВ
ЃЌЧѓдВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊдВ![]() гы
гы![]() жсЯрЧаЃЌдВаФдкжБЯп
жсЯрЧаЃЌдВаФдкжБЯп![]() ЩЯЃЌЧвдВ
ЩЯЃЌЧвдВ![]() БЛжБЯп
БЛжБЯп![]() НиЕУЕФЯвГЄЮЊ
НиЕУЕФЯвГЄЮЊ![]() ЃЌЧѓдВ
ЃЌЧѓдВ![]() ЕФЗНГЬЃЎ
ЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЖрбЁЬтЃЉЩше§ЪЕЪ§![]() Тњзу
Тњзу![]() ЃЌдђЃЈЃЉ
ЃЌдђЃЈЃЉ
A. ![]() газюаЁжЕ4B.
газюаЁжЕ4B. ![]() газюаЁжЕ
газюаЁжЕ![]()
C. ![]() газюДѓжЕ
газюДѓжЕ![]() D.
D. ![]() газюаЁжЕ
газюаЁжЕ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЭждВ![]() ЃК
ЃК![]() гыдВ
гыдВ![]() ЃК
ЃК![]() ЯрЧаЃЌВЂЧвЭждВ
ЯрЧаЃЌВЂЧвЭждВ![]() ЩЯЖЏЕугыдВ
ЩЯЖЏЕугыдВ![]() ЩЯЖЏЕуМфОрРызюДѓжЕЮЊ
ЩЯЖЏЕуМфОрРызюДѓжЕЮЊ![]() .
.

ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() зїСНЬѕЛЅЯрДЙжБЕФжБЯп
зїСНЬѕЛЅЯрДЙжБЕФжБЯп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгк
НЛгк![]() СНЕуЃЌ
СНЕуЃЌ![]() гыдВ
гыдВ![]() ЕФСэвЛНЛЕуЮЊ
ЕФСэвЛНЛЕуЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЃЌВЂЧѓШЁЕУзюДѓжЕЪБжБЯп
УцЛ§ЕФзюДѓжЕЃЌВЂЧѓШЁЕУзюДѓжЕЪБжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() гыжБЯп
гыжБЯп![]() ЯрЧаЃЌдВаФдк
ЯрЧаЃЌдВаФдк![]() жсЩЯЃЌЧвжБЯп
жсЩЯЃЌЧвжБЯп![]() БЛдВ
БЛдВ![]() НиЕУЕФЯвГЄЮЊ
НиЕУЕФЯвГЄЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓдВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() зїаБТЪЮЊ
зїаБТЪЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() гыдВ
гыдВ![]() НЛгк
НЛгк![]() СНЕуЃЌШєжБЯп
СНЕуЃЌШєжБЯп![]() гы
гы![]() ЕФаБТЪГЫЛ§ЮЊ
ЕФаБТЪГЫЛ§ЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com