
【题目】已知直线l:![]() 与拋物线C:
与拋物线C:![]() 相切.
相切.
(1)求拋物线方程;
(2)斜率不为0的直线![]() 经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线
经过拋物线C的焦点F,交抛物线于两点A,B,拋物线C上是否存在两点D,E关于直线![]() 对称.若存在求出斜率k的取值范围;若不存在,说明理由.
对称.若存在求出斜率k的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析
;(2)不存在,理由见解析
【解析】
(1)联立直线的方程和抛物线方程,利用判别式为零列方程,解方程求得![]() ,由此求得抛物线方程.
,由此求得抛物线方程.
(2)设出直线![]() 的方程,根据对称性设出直线
的方程,根据对称性设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和抛物线方程,化简后写出根与系数关系以及判别式,由此求得
的方程和抛物线方程,化简后写出根与系数关系以及判别式,由此求得![]() 中点
中点![]() 的坐标,将
的坐标,将![]() 点坐标代入直线
点坐标代入直线![]() 的方程,化简后判断出符合题意的
的方程,化简后判断出符合题意的![]() 不存在.
不存在.
![]() 由题联立方程组
由题联立方程组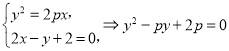 .
.
因为直线l与拋物C相切,所以![]() ,
,![]() 舍
舍![]() ,
,
所以抛物线C的方程为![]() .
.
![]() 由
由![]() 可知
可知![]() ,所以可设直线
,所以可设直线![]() 的方程为
的方程为![]() .
.
假设抛物线C上存在两点D,E关于直线![]() 对称,
对称,
可设直线DE的方程为![]() ,
,
联立方程组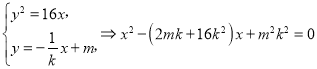 .
.
由![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,DE中点为
,DE中点为![]() ,
,
则![]() ,
,![]() ,
,
因为![]() 在直线
在直线![]() 上,所以将其代入方程
上,所以将其代入方程![]() ,
,
得![]() ,即
,即![]() ,
,
代入![]() ,得
,得![]() ,
,
所以k无解,故不存在.
即抛物线C上不存在两点D,E关于过焦点的直线![]() 对称.
对称.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,有下列四个命题,其中正确的有( )
,有下列四个命题,其中正确的有( )
A.对于![]() (
(![]() ,0),函数
,0),函数![]() 在
在![]() 上是单调增函数
上是单调增函数
B.对于![]() (0,
(0,![]() ),函数
),函数![]() 存在最小值
存在最小值
C.存在![]() (
(![]() ,0),使得对于任意
,0),使得对于任意![]() ,都有
,都有![]() 成立
成立
D.存在![]() (0,
(0,![]() ),使得函数
),使得函数![]() 有两个零点
有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从5名男生和4名女生中选出4人参加辩论比赛.
(1)如果男生中的甲与女生中的乙至少要有1人在内,那么有多少种不同选法?
(2)如果4个人中既有男生又有女生,那么有多少种不同选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某林场现有木材存量为![]() ,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为
,每年以25%的增长率逐年递增,但每年年底要砍伐的木材量为![]() ,经过
,经过![]() 年后林场木材存有量为
年后林场木材存有量为![]()
(1)求![]() 的解析式
的解析式
(2)为保护生态环境,防止水土流失,该地区每年的森林木材存量不应少于![]() ,如果
,如果![]() ,那么该地区会发生水土流失吗?若会,要经过几年?(取
,那么该地区会发生水土流失吗?若会,要经过几年?(取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
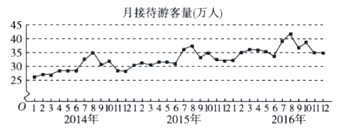
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,把函数
)的部分图象如图所示,把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像。
的图像。

(1)当![]() 时,若方程
时,若方程![]() 恰好有两个不同的根
恰好有两个不同的根![]() ,求
,求![]() 的取值范围及
的取值范围及![]() 的值;
的值;
(2)令![]() ,若对任意
,若对任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com