
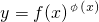 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得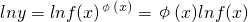 ,两边对x求导数,得
,两边对x求导数,得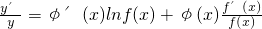 ,于是
,于是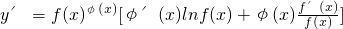 ,运用此方法可以求得函数
,运用此方法可以求得函数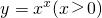 在(1,1)处的切线方程是________.
在(1,1)处的切线方程是________.科目:高中数学 来源:2012-2013学年江苏省高三下学期期中考试数学试卷(解析版) 题型:填空题
我们把形如 的函数称为“莫言函数”,并把其与
的函数称为“莫言函数”,并把其与 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当
轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当 ,
, 时,在所有的“莫言圆”中,面积的最小值 .
时,在所有的“莫言圆”中,面积的最小值 .
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
我们把形如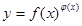 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得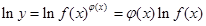 ,两边对
,两边对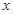 求导数,得
求导数,得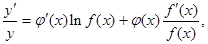 于是
于是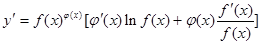 ,运用此方法可以求得函数
,运用此方法可以求得函数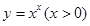 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第八次月考理科数学试卷 题型:填空题
我们把形如 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得 ,两边对x求导数,得
,两边对x求导数,得 于是
于是 ,运用此方法可以求得函数
,运用此方法可以求得函数 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三下学期2月联考理科数学 题型:填空题
我们把形如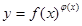 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得 ,两边对x求导数,得
,两边对x求导数,得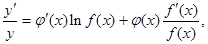 于是
于是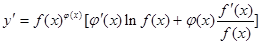 ,运用此方法可以求得函数
,运用此方法可以求得函数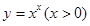 在(1,1)处的切线方程是 ▲
.
在(1,1)处的切线方程是 ▲
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省高三期中考试数学卷 题型:选择题
Ⅰ(理)我们把形如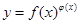 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得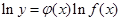 ,两边求导数,得
,两边求导数,得
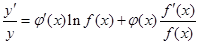 ,于是
,于是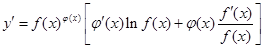 ,运用此方法可以探求得函数
,运用此方法可以探求得函数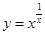 的一个单调递增区间是
的一个单调递增区间是
A.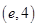 B.
B.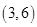 C.
C.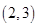 D.
D. 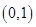
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com