
已知函数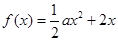 ,
, .
.
(1)如果函数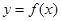 在
在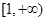 上是单调减函数,求
上是单调减函数,求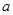 的取值范围;
的取值范围;
(2)是否存在实数 ,使得方程
,使得方程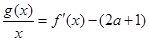 在区间
在区间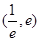 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出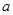 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)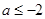 (2)
(2)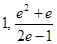
解析试题分析:解:(1)当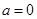 时,
时,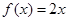 在
在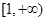 上是单调增函数,不符合题意.…1分
上是单调增函数,不符合题意.…1分
当 时,
时,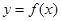 的对称轴方程为
的对称轴方程为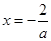 ,由于
,由于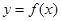 在
在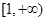 上是单调增函数,不符合题意.
上是单调增函数,不符合题意.
当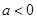 时,函数
时,函数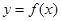 在
在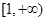 上是单调减函数, 则
上是单调减函数, 则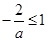 ,解得
,解得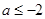 ,
,
综上,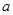 的取值范围是
的取值范围是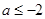 . 4分
. 4分
(2)把方程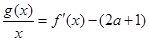 整理为
整理为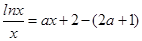 ,
,
即为方程 . 5分
. 5分
设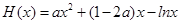
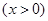 ,原方程在区间(
,原方程在区间(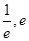 )内有且只有两个不相等的实数根, 即为函数
)内有且只有两个不相等的实数根, 即为函数 在区间(
在区间(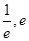 )内有且只有两个零点. ……6分
)内有且只有两个零点. ……6分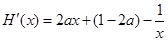
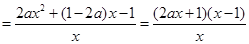 7分
7分
令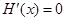 ,因为
,因为 ,解得
,解得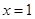 或
或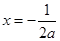 (舍) 8分
(舍) 8分
当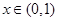 时,
时, 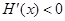 ,
,  是减函数;
是减函数;
当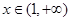 时,
时, 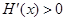 ,
, 是增函数.……10分
是增函数.……10分 在(
在(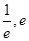 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需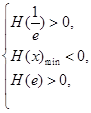 13分
13分
即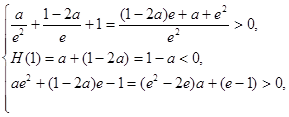 ∴
∴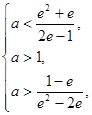
解得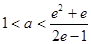 , 所以
, 所以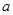 的取值范围是(
的取值范围是(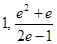 ) . 14分
) . 14分
考点:导数的应用
点评:解决的关键是通过导数的符号判定函数但典型,进而来解决方程根的问题,以及函数单调性的应用,属于基础题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
设函数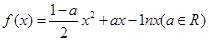 。
。
(1)当a=l时,求函数 的极值;
的极值;
(2)当a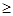 2时,讨论函数
2时,讨论函数 的单调性;
的单调性;
(3)若对任意a∈(2,3)及任意x1,x2∈[1,2],恒有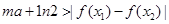 成立,求
成立,求
实数m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com