
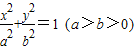 的长轴为AB,过点B的直线l与x轴垂直.直线(2-k)x-(1+2k)y+(1+2k)=0(k∈R)所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
的长轴为AB,过点B的直线l与x轴垂直.直线(2-k)x-(1+2k)y+(1+2k)=0(k∈R)所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率 .
.
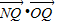 求得结果为0,进而可推知OQ⊥QN,推断出直线QN与圆O相切.
求得结果为0,进而可推知OQ⊥QN,推断出直线QN与圆O相切.
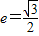 得a=2.
得a=2.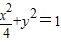 .
.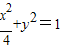 .
.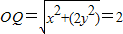
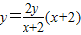 .
.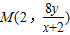 .又B(2,0),N为MB的中点,
.又B(2,0),N为MB的中点, .
.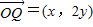 ,
,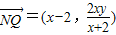 .
.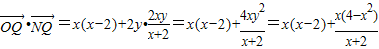
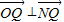 .∴直线QN与圆O相切.
.∴直线QN与圆O相切.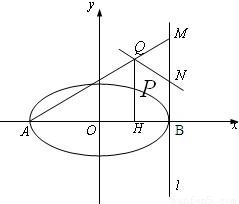


科目:高中数学 来源: 题型:
 (2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0
(2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0| k1x1x2 |
| x1+x2 |
| k1x3x4 |
| x3+x4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(03年北京卷理)(15分)
如图,已知椭圆的长轴![]() 与
与![]() 轴平行,短轴
轴平行,短轴![]() 在
在![]() 轴上,中心
轴上,中心![]() (
(![]()
(Ⅰ)写出椭圆方程并求出焦点坐标和离心率;
(Ⅱ)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() (
(![]() ),直线
),直线![]() 与椭圆次于
与椭圆次于![]() ,
,![]() (
(![]() ).求证:
).求证:![]() ;
;
(Ⅲ)对于(Ⅱ)中的在![]() ,设
,设![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() 交
交![]() 轴于
轴于![]() 点,求证:
点,求证:![]() (证明过程不考虑
(证明过程不考虑![]() 或
或![]() 垂直于
垂直于![]() 轴的情形)
轴的情形)

查看答案和解析>>
科目:高中数学 来源: 题型:
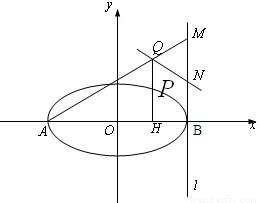
如图,已知椭圆![]() 的长轴
的长轴![]() ,离心率
,离心率![]() ,
,![]() 为坐标原点,过
为坐标原点,过![]() 的直线
的直线![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,
的任意一点,![]() ,
,![]() 为垂足,延长
为垂足,延长![]() 至
至![]() ,使得
,使得![]() ,连接
,连接![]() 并延长交直线
并延长交直线![]() 于
于![]() ,
,![]() 为
为![]() 的中点
的中点
(1)求椭圆方程并证明![]() 点在以
点在以![]() 为直径的圆
为直径的圆![]() 上
上
(2)试判断直线![]() 与圆
与圆![]() 的位置关系
的位置关系
 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江高三上期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,已知椭圆 的长轴为
的长轴为 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率

(1)求椭圆的标准方程;
(2)设 是椭圆上异于
是椭圆上异于 、
、 的任意一点,
的任意一点, 轴,
轴, 为垂足,延长
为垂足,延长 到点
到点 使得
使得 ,连接
,连接 并延长交直线
并延长交直线 于点
于点 ,
, 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 为直径的圆
为直径的圆 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省哈尔滨市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图,已知椭圆 的长轴为
的长轴为 ,过点
,过点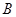 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
(1)求椭圆的标准方程;
(2)设 是椭圆上异于
是椭圆上异于 、
、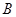 的任意一点,
的任意一点, 轴,
轴, 为垂足,延长
为垂足,延长 到点
到点 使得
使得 ,连接
,连接 并延长交直线
并延长交直线 于点
于点 ,
, 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 为直径的圆
为直径的圆 的位置关系.
的位置关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com