
【题目】若数列![]() 满足:对于任意
满足:对于任意![]() 均为数列
均为数列![]() 中的项,则称数列
中的项,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 的前
的前![]() 项和
项和![]() ,求证:数列
,求证:数列![]() 为“
为“![]() 数列”;
数列”;
(2)若公差为![]() 的等差数列
的等差数列![]() 为“
为“![]() 数列”,求
数列”,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 为“
为“![]() 数列”,
数列”,![]() ,且对于任意
,且对于任意![]() ,均有
,均有![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)先利用项和公式计算出an=4n-2,再利用“![]() 数列”证明.(2)利用“
数列”证明.(2)利用“![]() 数列”的性质求
数列”的性质求![]() 的取值范围.(3)先证明数列{an}为等差数列,再转化an<a
的取值范围.(3)先证明数列{an}为等差数列,再转化an<a![]() -a<an+1,再转化为n(2t2-t)>t2-3t+1,n(t-2t2)>2t-t2-1,分析得到公差t=
-a<an+1,再转化为n(2t2-t)>t2-3t+1,n(t-2t2)>2t-t2-1,分析得到公差t=![]() ,求出数列
,求出数列![]() 的通项公式.
的通项公式.
详解:(1)当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
又a1=S1=2=4×1-2,所以an=4n-2.
所以an+|an+1-an+2|=4n-2+4=4(n+1)-2为数列{an}的第n+1项,
因此数列{an}为“T 数列”.
(2)因为数列{an}是公差为d的等差数列,
所以an+|an+1-an+2|=a1+(n-1) d+|d|.
因为数列{an}为“T 数列”,
所以任意n∈N*,存在m∈N*,使得a1+(n-1) d+|d|=am,即有(m-n) d=|d|.
①若d≥0,则存在m=n+1∈N*,使得(m-n) d=|d|,
②若d<0,则m=n-1.
此时,当n=1时,m=0不为正整数,所以d<0不符合题意. 综上,d≥0.
(3)因为an<an+1,所以an+|an+1-an+2|=an+an+2-an+1.
又因为an<an+an+2-an+1=an+2-(an+1-an)<an+2,且数列{an}为“T数列”,
所以an+an+2-an+1=an+1,即an+an+2=2an+1,
所以数列{an}为等差数列.
设数列{an}的公差为t(t>0),则有an=1+(n-1)t,
由an<a![]() -a<an+1,得1+(n-1)t<t[2+(2n-1)t]<1+nt,
-a<an+1,得1+(n-1)t<t[2+(2n-1)t]<1+nt,
整理得n(2t2-t)>t2-3t+1, ①
n(t-2t2)>2t-t2-1. ②
若2t2-t<0,取正整数N0>![]() ,
,
则当n>N0时,n(2t2-t)<(2t2-t) N0<t2-3t+1,与①式对于任意n∈N*恒成立相矛盾,
因此2t2-t≥0.
同样根据②式可得t-2t2≥0,
所以2t2-t=0.又t>0,所以t=![]() .
.
经检验当t=![]() 时,①②两式对于任意n∈N*恒成立,
时,①②两式对于任意n∈N*恒成立,
所以数列{an}的通项公式为an=1+![]() (n-1)=
(n-1)=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
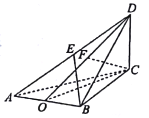
【题目】[2018·郴州期末]已知三棱锥![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到定点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2,设动点P的轨迹为曲线C.
的距离小2,设动点P的轨迹为曲线C.
![]() 求曲线C的方程;
求曲线C的方程;
![]() 若直线
若直线![]() 与曲线C和圆
与曲线C和圆![]() 从左至右的交点依次为A,B,C,D求
从左至右的交点依次为A,B,C,D求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①命题“任意![]() ”的否定是“任意
”的否定是“任意![]() ;
;
②命题“若![]() ,则
,则![]() ”的逆否命题是真命题;
”的逆否命题是真命题;
③若命题![]() 为真,命题
为真,命题![]() 为真,则命题
为真,则命题![]() 且
且![]() 为真;
为真;
④命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”.
”.
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门对某工厂甲、乙两个车间生产的12个零件质量进行检测.甲、乙两个车间的零件质量(单位:克)分布的茎叶图如图所示.零件质量不超过20克的为合格.
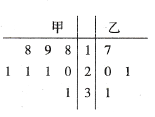
(1)从甲、乙两车间分别随机抽取2个零件,求甲车间至少一个零件合格且乙车间至少一个零件合格的概率;
(2)质检部门从甲车间8个零件中随机抽取4件进行检测,若至少2件合格,检测即可通过,若至少3 件合格,检测即为良好,求甲车间在这次检测通过的条件下,获得检测良好的概率;
(3)若从甲、乙两车间12个零件中随机抽取2个零件,用![]() 表示乙车间的零件个数,求
表示乙车间的零件个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品的保鲜时间y(单位:小时)与储存温度x(单位:![]() )满足函数关系
)满足函数关系![]() (k,m为常数).若该食品在0
(k,m为常数).若该食品在0![]() 的保鲜时间是64小时,在18
的保鲜时间是64小时,在18![]() 的保鲜时间是16小时,则该食品在36
的保鲜时间是16小时,则该食品在36![]() 的保鲜时间是( )
的保鲜时间是( )
A.4小时B.8小时C.16小时D.32小时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探究函数![]() ,
,![]() 上的最小值,并确定取得最小值时
上的最小值,并确定取得最小值时![]() 的值,列表如下:
的值,列表如下:
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 14 | 7 | 5.34 | 5.11 | 5.01 | 5 | 5.01 | 5.04 | 5.08 | 5.67 | 7 | 8.6 | 12.14 | … |
(1)观察表中![]() 值随
值随![]() 值变化趋势特点,请你直接写出函数
值变化趋势特点,请你直接写出函数![]() ,
,![]() 的单调区间,并指出当
的单调区间,并指出当![]() 取何值时函数的最小值为多少;
取何值时函数的最小值为多少;
(2)用单调性定义证明函数![]() 在
在![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·江西联考]交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
| |
数量 | 20 | 10 | 10 | 20 | 15 | 5 |
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() .某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
.某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com