
已知函数 .
.
(I)判断 的奇偶性;
的奇偶性;
(Ⅱ)设函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的表达式;
的表达式;
(Ⅲ)若 ,证明:方程
,证明:方程 有两个不同的正数解.
有两个不同的正数解.
(I)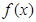 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
(Ⅱ)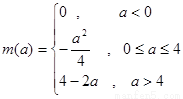 (Ⅲ)见解析
(Ⅲ)见解析
【解析】(1)对参数a进行讨论,利用奇偶函数的定义,即可得出结论;
(2)当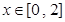 时,
时,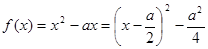 ,然后转化为二次函数轴动区间定的最值问题来研究即可.
,然后转化为二次函数轴动区间定的最值问题来研究即可.
(3)利用图像法,把方程根的个数转化为两个函数图像交点的个数来研究.
当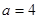 ,若
,若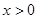 时,
时,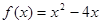 ,方程可化为
,方程可化为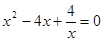 即
即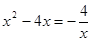 .
.
|
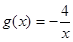 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数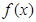 ,
,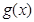 在
在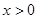 时的图像从图像确定函数
时的图像从图像确定函数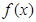 与
与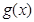 的图像在第四象限有两个不同交点,从而证明方程
的图像在第四象限有两个不同交点,从而证明方程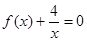 有两个不同的正数解.
有两个不同的正数解.
解:(I)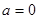 时,
时,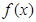 是奇函数;……(1分)
是奇函数;……(1分)
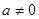 时,
时,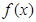 既不是奇函数也不是偶函数.……(2分)
既不是奇函数也不是偶函数.……(2分)
(II)当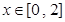 时,
时,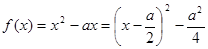 ,函数
,函数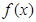 图像的对称轴为直线
图像的对称轴为直线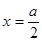 .(3分)
.(3分)
当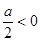 ,即
,即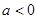 时,函数
时,函数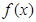 在
在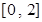 上是增函数,所以
上是增函数,所以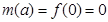 ;
;
当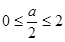 ,即
,即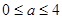 时,函数
时,函数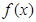 在
在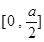 上是减函数,在
上是减函数,在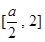 上是增函数,
上是增函数,
所以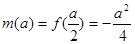 ;……(5分)
;……(5分)
当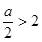 ,即
,即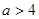 时,函数
时,函数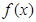 在
在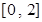 上是减函数,
上是减函数,
所以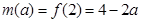 .……(6分)
.……(6分)
综上,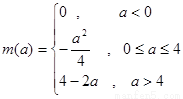 .……(7分)
.……(7分)
(III)证法一:
若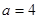 ,则
,则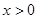 时,
时,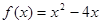 ,方程可化为
,方程可化为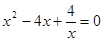 ,
,
即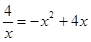 .……(8分)
.……(8分)
令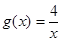 ,
,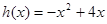 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数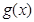
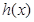 在
在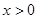 时的图像…(9分)
时的图像…(9分)

因为 ,
,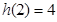 ,所以
,所以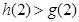 ,即当
,即当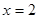 时
时
函数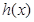 图像上的点在函数
图像上的点在函数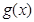 图像点的上方.……(11分)
图像点的上方.……(11分)
所以函数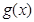 与
与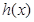 的图像在第一象限有两个不同交点.
的图像在第一象限有两个不同交点.
即方程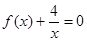 有两个不同的正数解.…………(12分)
有两个不同的正数解.…………(12分)
证法二:
若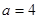 ,则
,则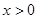 时,
时,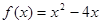 ,方程可化为
,方程可化为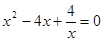 ,
,
即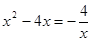 .…………(8分)
.…………(8分)
|
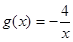 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数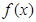 ,
,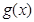 在
在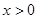 时的图像.(9分)
时的图像.(9分)
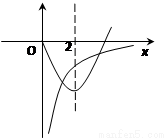
因为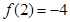 ,
,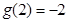 ,所以
,所以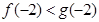 ,
,
即当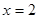 时,函数
时,函数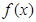 图像上的点在函数
图像上的点在函数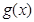 图像点的上方.…………(11分)
图像点的上方.…………(11分)
所以函数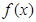 与
与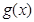 的图像在第四象限有两个不同交点.
的图像在第四象限有两个不同交点.
所以方程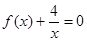 有两个不同的正数解.…………(12分)
有两个不同的正数解.…………(12分)


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模文)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当![]() 变化且直线
变化且直线![]() 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线![]() 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式![]() ;当
;当![]() 且P与M重合时,求
且P与M重合时,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模理)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模理)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线![]() ,抛物线
,抛物线![]() ,
,
定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当![]() 变化且直线
变化且直线![]() 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线![]() 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式![]() ;若P与M重合时,求
;若P与M重合时,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com